Question

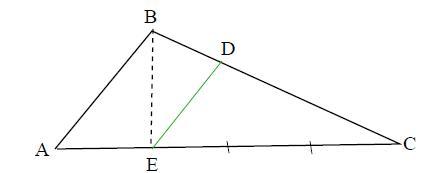
Реши задачу. В треугольнике ABC точка Е делит сторону AC в отношении 3:1, считая от вершины С. Отрезки ED и AB параллельны. Найди AB, если ED = 9. ​

Answer 1

Ответ:

АВ = 12

Объяснение:

Дано:

ΔАВС

АЕ : ЕС = 1 : 3

ED || AB

ED = 9

AB - ?

-----------------------

1) Прямая, параллельная основанию, отсекает треугольник, подобный данному, т.е.

ΔАВС ~ ΔEDC, т.к. ED || AB

В подобных треугольниках отношение длин соответствующих элементов равно коэффициенту подобия:

АС : ЕС = k = AB : ED

(3 +1) : 3 = 4 : 3 = AB : 9, откуда

АВ = 4*9/3 = 12