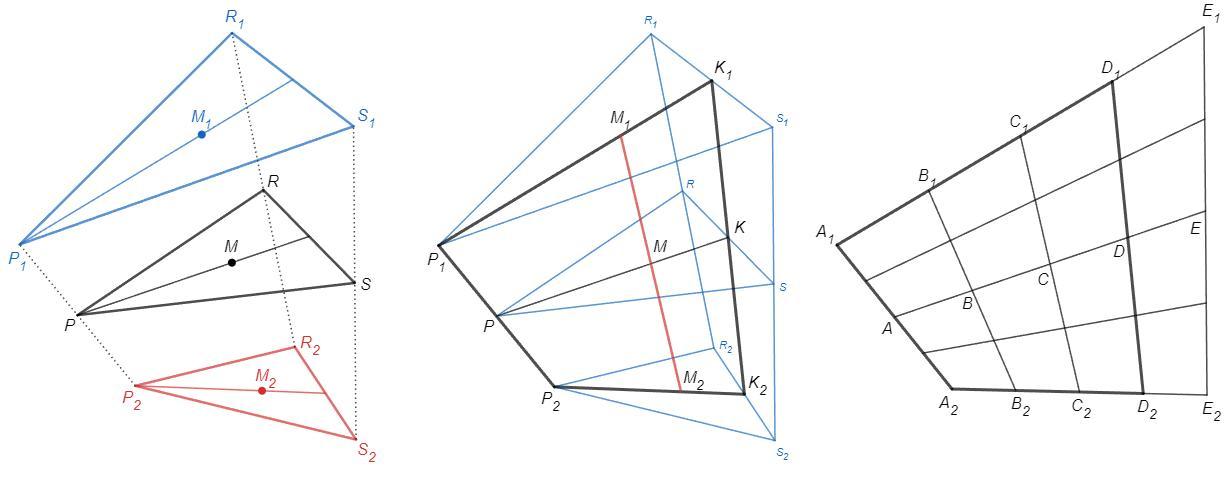
Даны три треугольника: PRS, P1R1S1, P2R2S2. Известно, что P - середина отрезка P1P2, R - середина отрезка R1R2, S - середина отрезка S1S2, M - точка пересечения медиан треугольника PRS, M1 - точка пересечения медиан треугольника P1R1S1, M2 - точка пересечения медиан треугольника P2R2S2. Докажите, что точки M, M1, M2 лежат на одной прямой.
Ответы
Рассмотрим произвольный выпуклый четырехугольник A1E1E2A2.
A, E, C1, C2 - середины сторон,
AC1EC2 - параллелограмма Вариньона,
C - середина диагоналей AE и С1С2.
Теперь рассмотрим A1С1С2A2. Аналогично, B - середина AC и B1B2.
Продолжая построение, получим сетку из равных отрезков на каждой прямой. Из равных отрезков можно собрать любое отношение.
Вывод:
Если на противоположных сторонах четырехугольника отметить точки C1, C2, A, D такие, что
A1C1/C1D1=A2C2/C2D2=х ; A1A/АА2=D1D/DD2=y
то AC/CD=x ; СС1/СС2=у
Пусть K, K1, K2 - середины RS, R1S1, R2S2
RK1SK2 - параллелограмм Вариньона четырехугольника R1S1S2R2
=> K - середина K1K2
Рассмотрим P1K1K2P2 и пересечение отрезков M1M2 и PK
P1P/PP2 =K1K/KK2, P1M1/M1K1 =P2M2/M2K2 =2/1 (пересечение медиан)
=> PM/MK =2/1
т.е. M - точка пересечения медиан PRS