Алексею с братом в наследство от отца достался прямоугольный участок площадью
4800 м?. Никто из братьев не хотел отказываться от наследства, а потому они решили поделить участок пополам. Но необычным образом: по диагонали. В результате Алексею достался участок вдвое меньшей площадью (2400 м?) в форме прямоугольного треугольника.
Выяснилось, что периметр образовавшегося участка (периметр треугольника) равен 240 м. А чему в этом случае равны его стороны?
В ответ запишите длины сторон в метрах в порядке возрастания через пробел.
Ответы
Ответ:
Стороны треугольника равны 60 м и 80 м.
Пошаговое объяснение:
Алексею с братом в наследство от отца достался прямоугольный участок площадью 4800 м². Никто из братьев не хотел отказываться от наследства, а потому они решили поделить участок пополам. Но необычным образом: по диагонали. В результате Алексею достался участок вдвое меньшей площадью (2400 м²) в форме прямоугольного треугольника.
Выяснилось, что периметр образовавшегося участка (периметр треугольника) равен 240 м. А чему в этом случае равны его стороны?
- Площадь прямоугольника равна произведению смежных сторон.
- Периметр треугольника равен сумме длин всех сторон.
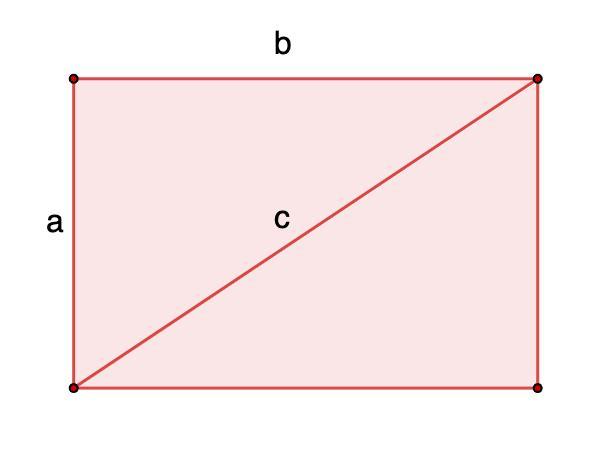
Пусть стороны прямоугольника равна а и b, а диагональ равна с.
Тогда площадь прямоугольника равна
S = ab = 4800 м²
Из прямоугольного треугольника по теореме Пифагора:
a² + b² = c²
Дополним до полного квадрата:
a² + 2ab + b² - 2ab = c²
(a + b)² - 2ab = c²
ab = 4800 ⇒
(a + b)² - 9600 = c² (1)
Периметр прямоугольника равен:
Р = a + b + c = 240 м
или
(a + b) + c = 240 (2)
Пусть (а + b) = x
Тогда из (1) и (2) получим систему:
Получили a + b = 140, a ab = 4800.
Решим эту систему:
Тогда
Стороны треугольника равны 60 м и 80 м.
#SPJ1