Предмет: Геометрия,
автор: movyle
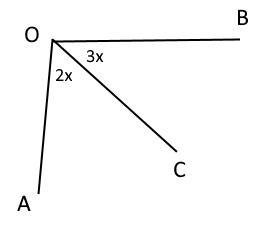
Між сторонами кута AOB, що дорівнює 95 градусів, проходить промінь OC. Знайти кути AOC, і COB, якщо міри цих кутів відносяться, як 2:3
Ответы
Автор ответа:
1
Ответ:
Дано: ∠AOB = 95,
OC є ∠AOB,
∠AOC : ∠COB = 2 : 3
∠AOC = ?, ∠COB = ?
∠AOC : ∠COB = 2 : 3 (за умовою)
Нехай x - 1 частина
∠AOC = 2x
∠COB = 3x
∠AOB = ∠AOC + ∠COB (за властивістю вимірювання кутів)
∠AOB = 95
∠AOC + ∠COB = 95
2x + 3x = 95
5x = 95
x = 19
∠AOC = 19 x 2 = 38
∠COB = 19 x 3 = 57
Объяснение:
Нам дано відношення кутів один до одного. Тобто, ми це можемо позначити за частини.
∠AOC - 2 частини
∠COB - 3 частини
1 частину позначаємо за x і получаємо просте рівняння.
Приложения:
movyle:
Дуже вдячна за рішення
Похожие вопросы
Предмет: Английский язык,
автор: dashgon
Предмет: Математика,
автор: anabobricka2
Предмет: Английский язык,
автор: volkova1979
Предмет: Английский язык,
автор: Horoh123
Предмет: Математика,
автор: glebkordukov777