Помогите, не могу решить данный треугольник
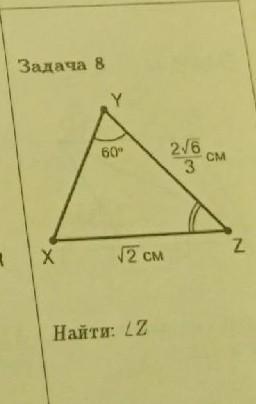
Ответы
Ответ:
Пошаговое объяснение:
Теорема косинусов:
квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a² = b² + c² - 2bc cosα → cosα = ( b² + c² - a²)/2bc
1) Примем, что сторона ху = b, тогда
(√2)² = b² + (2√6/3)² - 2 * b * 2√6/3 * cos60°
т.к. cos60° = 1/2, то
2 = b² + 4 *6/9 - (4b√6/3) *1/2
b² - 2b√6/3 + 8/3 - 2 = 0
b² - 2*b * √6/3 + (√6 / 3)² - (√6 / 3)² + 2/3 = 0
(b - √6/3)² - 6/9 + 2/3 = 0
(b - √6/3)² - 2/3 + 2/3 = 0
(b - √6/3)² = 0
b = √6/3
2) cos (Z) = [(2√6/3)² + (√2)² - (√6/3)²] : 2*2√6/3 * √2 =
= (24/9 + 2 - 6/9) / 4√12 / 3 = (8/3 - 2/3 + 2)* 3 / 8√3 = (2+2)*3/8√3 =
= 12/8√3 = 3/2√3 = 3*√3/ 2*3 = √3/2
cos (Z) = √3/2 - это угол в 30°, т.е.
∠Z = 30°