Предмет: Алгебра,
автор: grisenkovalerij80
допоможіть будь ласка
Приложения:
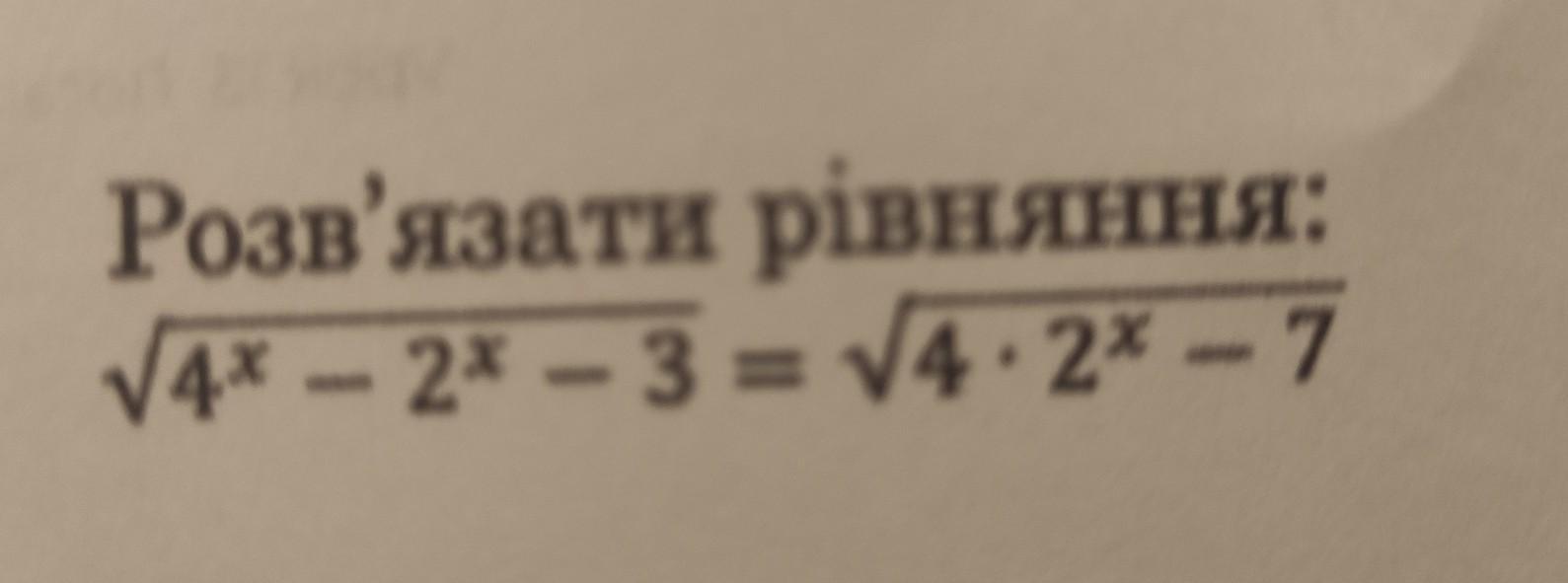
Ответы
Автор ответа:
1
Ответ:
Иррациональное уравнение .
Возведём в квадрат обе части равенства .
Замена:
Перейдём к старой переменной .
Проверка:
подкоренное выражение не
может быть отрицательным . Поэтому х=0 не является корнем уравнения .
При подстановке х=2 и левая часть равенства и правая равны одному и тому же числу 3 . Значит, х=2 является корнем уравнения .
Ответ: х=2 .
Похожие вопросы
Предмет: Химия,
автор: zayachukrodion
Предмет: Математика,
автор: dokidoki2206
Предмет: Физика,
автор: jekalolban226
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: Аноним