Предмет: Геометрия,
автор: melnykvlad28
Надо решить номер 143 СРОЧНО
Приложения:

Ответы
Автор ответа:
2
Ответ:
ВС₁ = 9см
Объснение:
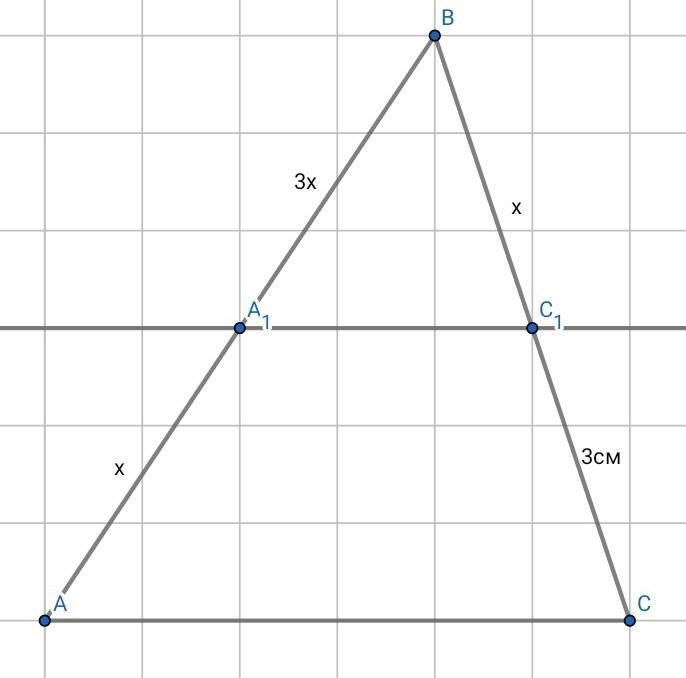
Задание: Прямая , паралельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках А₁ и С₁ соответственно. Найдите ВС₁ , если СС₁ = 3см , ВА₁ : АА₁ = 3 : 1
Дано : А₁С₁||АС , А₁∈АВ , С₁∈ВС , СС₁ = 3см , ВА₁ : АА₁ = 3 : 1
Найти : ВС₁
Решение:
При паралельных отрезков ∆АВС ~ ∆А₁ВС₁ , ∠В - общий , по второму признаку подобия треугольников : Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Возьмём сторону ВС₁ за "x" и составим пропорцию:
По условию ВА₁ : АА₁ = 3 : 1 , СС₁ = 3см
Приложения:
Похожие вопросы
Предмет: Литература,
автор: yurchakanastasiia
Предмет: Математика,
автор: grischenkoarina2011
Предмет: Экономика,
автор: SofiaSofia7
Предмет: География,
автор: ignatcev
Предмет: Музыка,
автор: mariakambaratova