Question

биссектриса внутреннего угла А треугольника ABC пересекает сторону BC в точке D, точка E на стороне AB такова, что угол adc = углу ade. известно что длина стороны AB равна 31 а длина стороны BC больше длины стороны на 9 Найдите периметр треугольника DEB​

Answer 1

Ответ:

Периметр треугольника DEB равен 40 единиц

Пошаговое объяснение:

Исправленное условие:

Биссектриса внутреннего угла А треугольника ABC пересекает сторону BC в точке D, точка E на стороне AB такова, что ∠ADC = ∠ADE. Известно что длина стороны AB равна 31, а длина стороны BC больше длины стороны AC на 9. Найдите периметр треугольника DEB​.

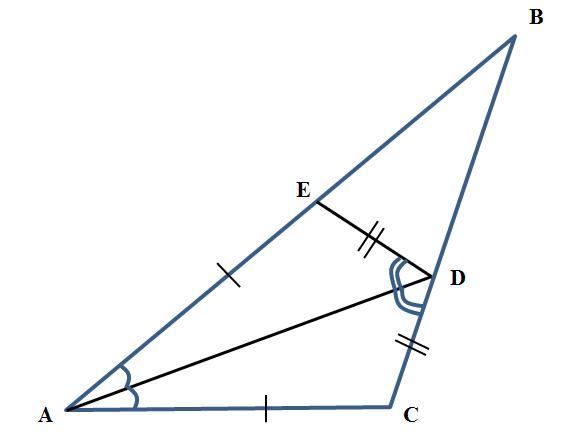
Дано: ΔАВС (см. рисунок).

 D∈ВC, АD - биссектриса;

 E∈АВ; ∠ADC = ∠ADE.

АВ = 31, ВС = AC + 9.  

Найти: Р(DEB).

Решение.

a) ΔADC = ΔADE по 2-признаку (по стороне и двум прилежащим к ней углам), так как:

1) Сторона AD - общая;

2) ∠EAD = ∠DAC (АD - биссектриса);

3) ∠ADC = ∠ADE (по условию задачи).

Тогда как соответствующие стороны:

DC = DE и AC = AE.

б) Периметр треугольника DEB:

Р(DEB) = ЕВ + BD + DE.

Но, по установленному выше:

EB = AB - AE = AB - AC,

BD + DE = BD + DC = BC = AC + 9.

Поэтому

Р(DEB) = AB - AC + AC + 9 = AB + 9 = 31 + 9 = 40.

Значит, периметр треугольника DEB равен 40 ед.

#SPJ1