Предмет: Алгебра,
автор: Efimenkoyana2006
ДОПОМОЖІТЬ ОЧЕНЬ СРОЧНО!!!!!!!!!!!
Приложения:
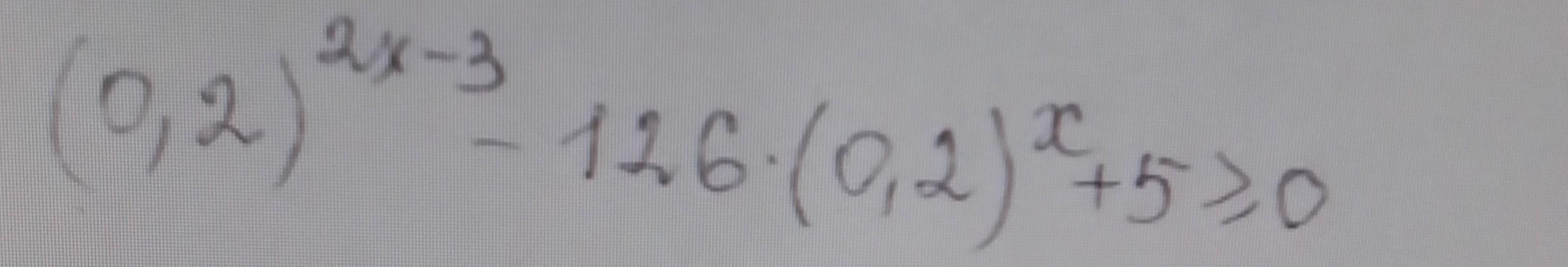
Efimenkoyana2006:
Показникові нерівності
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Введем замену
Отобразим на интервале
Теперь подставим
Сможете помочь мне с історией України????
Похожие вопросы
Предмет: Математика,
автор: honoport
Предмет: Математика,
автор: titarcukoksana9
Предмет: Қазақ тiлi,
автор: omurbaevzhalgas
Предмет: История,
автор: vkookieisreal