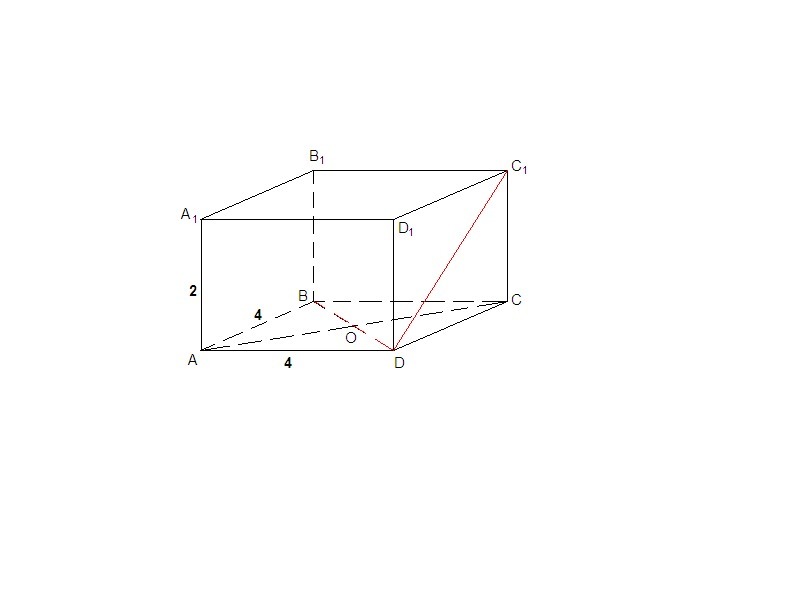
Измерения прямоугольного параллелепипеда равны 4, 4 и 2 см. Найдите расстояние от наименьшего ребра до наибольшей диагонали грани, скрещивающейся с ним.
Ответы
Все грани прямоугольного параллелепипеда - прямоугольники.
Пусть ребра основания равны 4 и 4 см, а боковое ребро 2 см.
Тогда боковое ребро - наименьшее ребро (все боковые ребра равны). Осталось выяснить, какая из диагоналей, скрещивающаяся с данным ребром, наибольшая.
Так как ребра основания равны, то боковые грани - равные прямоугольники. По теореме Пифагора вычислим диагональ одной боковой грани:
DC₁ = √(DC² + CC₁²) = √(16 + 4) = √20 = 2√5 см
Диагональ основания:
BD = √(AB² + AD²) = √(16 + 16) = √32 = 4√2 см
Диагональ основания больше. Значит надо найти расстояние от ребра АА₁ до BD.
АО⊥АА₁ так как ребро АА₁ перпендикулярно плоскости АВС, а АО лежит в этой плоскости,
АО⊥BD как диагонали квадрата, значит АО - искомое расстояние.
АО = 1/2BD = 1/2 · 4√2 = 2√2 см (так как диагонали квадрата равны и точкой пересечения делятся пополам)