Предмет: Алгебра,
автор: julia15asd
ДОПОМОЖІТЬ ДАЮ 30 БАЛІВ!
Приложения:
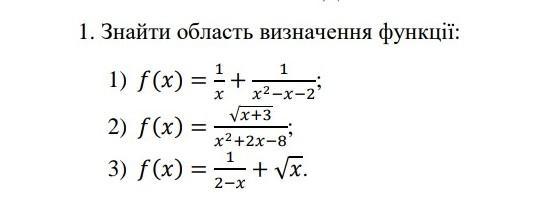
Ответы
Автор ответа:
0
Ответ:
Знаменатель дроби не может равняться 0 , а подкоренное выражение должно быть неотрицательным .
Похожие вопросы
Предмет: Геометрия,
автор: utkasolovas
Предмет: Математика,
автор: lalejc
Предмет: Українська мова,
автор: 2006maks2012
Предмет: Биология,
автор: Аноним
Предмет: Биология,
автор: Аноним