Предмет: Математика,
автор: sl47244
Встановити аналістичність комплексної функції w=F(z) i, якщо це можливо, обчислити значення її поідної у т. Z0
Приложения:
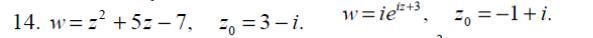
Ответы
Автор ответа:
1
Ответ:
1) Функция аналитическая и
2) Функция не аналитическая и не дифференцируема
Пошаговое объяснение:
По определению:
По определению комплексного числа:
По формуле Эйлера:
По теореме функция является однозначной аналитической функции одной комплексной переменной если для неё выполняются условия Коши — Римана (Даламбера — Эйлера):
Где и
— вещественная и мнимая части рассматриваемой функции.
14.
1)
- действительная часть
- мнимая часть
- условия Коши - Римана выполнены, следовательно функция
- аналитическая.
Так как функция аналитическая, то она является дифференцируемой.
2)
- действительная часть
- мнимая часть
- условия Коши - Римана не выполнены, следовательно функция
- не аналитическая и не дифференцируема.
Похожие вопросы
Предмет: Алгебра,
автор: OMirazhO
Предмет: Українська мова,
автор: tinamahu20
Предмет: Математика,
автор: s0368528
Предмет: Литература,
автор: Mishka228228288228
Предмет: Математика,
автор: ilyawinstonamazin