Предмет: Геометрия,
автор: 1lusha09
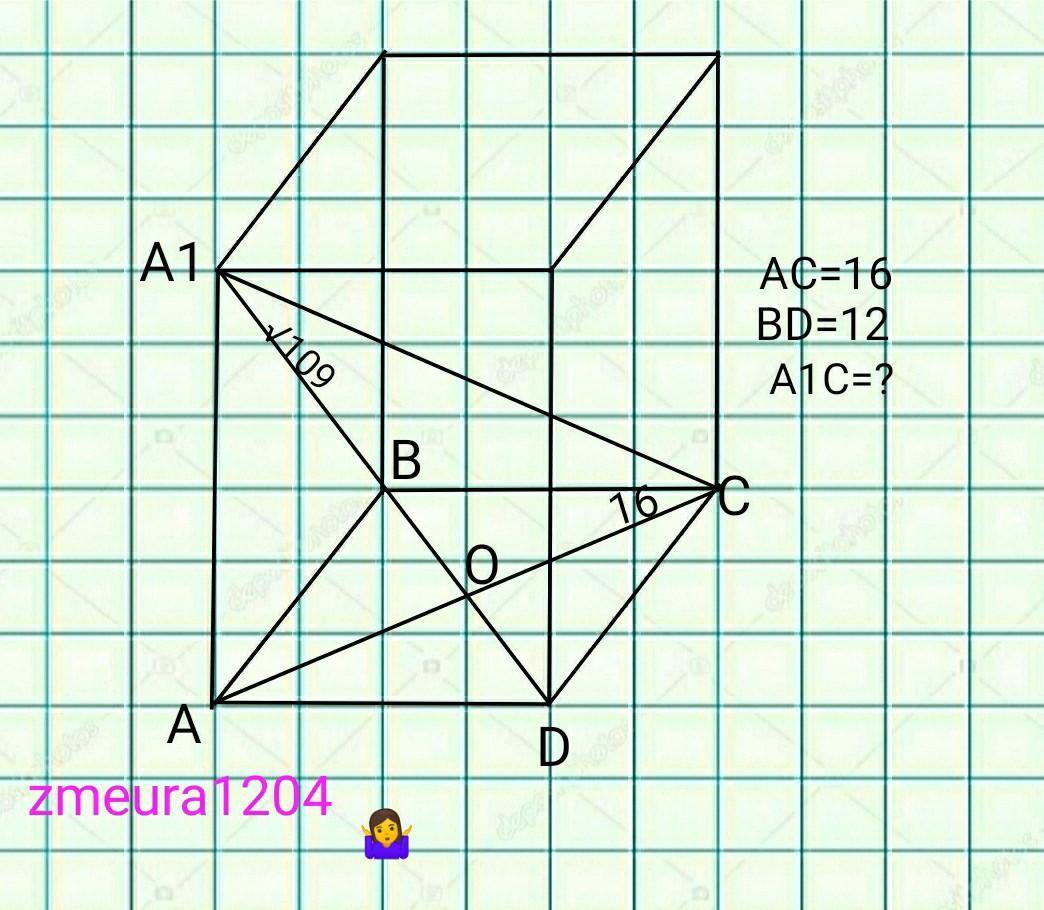
Основою прямого паралелепіпеда є ромб з діагоналями 12 і 16см. Діагональ бічної грані дорівнює √109 см. Знайти більшу діагональ паралелепіпеда і його бічну поверхню.
Ответы
Автор ответа:
7
Ответ:
Sбіч=120см²
А1С=√265см
Объяснение:
ВО=BD/2=12/2=6см
АО=АС/2=16/2=8см
∆АОВ- прямокутний трикутник.
За теоремою Піфагора:
АВ=√(ВО²+АО²)=√(6²+8²)=10см
AD=AB=10см свойство ромба.
∆А1АD- прямокутний трикутник.
За теоремою Піфагора
АА1=√(А1D²-AD²)=√((√109)²-10²)=
=√9=3см
Росн=4*АВ=4*10=40см
Sбіч=Росн*АА1=40*3=120см²
∆АА1С- прямокутний трикутник.
За теоремою Піфагора:
А1С=√(АА1²+АС²)=√(3²+16²)=
=√(9+256)=√265 см
Приложения:
Похожие вопросы
Предмет: Биология,
автор: avramenkoanzelika7
Предмет: Математика,
автор: julyjulyjuly133
Предмет: История,
автор: pasabojko591
Предмет: Русский язык,
автор: m3a4s3a