Докажите, что при любом значении сменной является правильным неравенство:(ответ обязательно должен быть с разъяснениями)
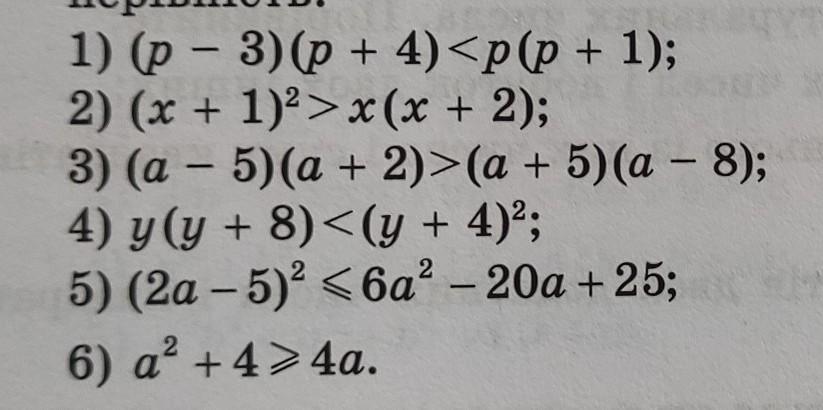
Ответы
Ответ:
отвеееееееееееееет на картинке

Ответ:
Объяснение:
1) (p - 3)((p + 4) < p((p+1)
Открываем скобки:
p² -3p +4p -12 <p² +p
Все члены с неизветным р переносим с противоположным знаком в левую часть неравенства, а все известные (числа) преносим в правую часть тоже с противоположным знаком:
p² -3p + 4p - p² - p < 12
0 < 12 - верно при любых р
2) (x +1)² > x(x + 2)
для (х+1)² применям формулу квадрата:(a + b)² = a² +2ab + b² :
x² +2x +1 > x² +2x
x² +2x +1 - x² -2x > 0
1>0 - верно при любых х
3) (a -5)(a +2) > (a+5)(a -8)
a² +2a -5a - 10 > a² +5a -8a - 40
a² -3a - 10> a² -3a - 40
a² -3a -a² +3a > -40 +10
0 > -30 - не может быть, неравенство неверно ни при каких а.
4) y(y+8) <(y + 4)²
y² +8y < y² +8y +16
0 < 16 - верно при любых у
5)(2a -5)² ≤ 6a² -20a +25
4a² -20a +25 - 6a² +20a ≤ 25
-2a² ≤ 25-25
-2a² ≤ 0 - верно при любых а, т.к. а² - число всегда положительное, а произведение положительного числа на число отрицат. всегда число отрицательное. При a = 0 → 0 = 0
6) a² + 4 ≥ 4a
a² - 4a + 4 ≥ 0
(a - 2)² ≥ 0 - верно при любых а
(а - 2)² всегда положительно, т,е. > 0
При а =2 → 0 = 0