Предмет: Математика,
автор: tioopf
Найдите значения других трёх основных тригонометрических функций, если
Приложения:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
применим основное тригонометрическое тождество
определим знак функции
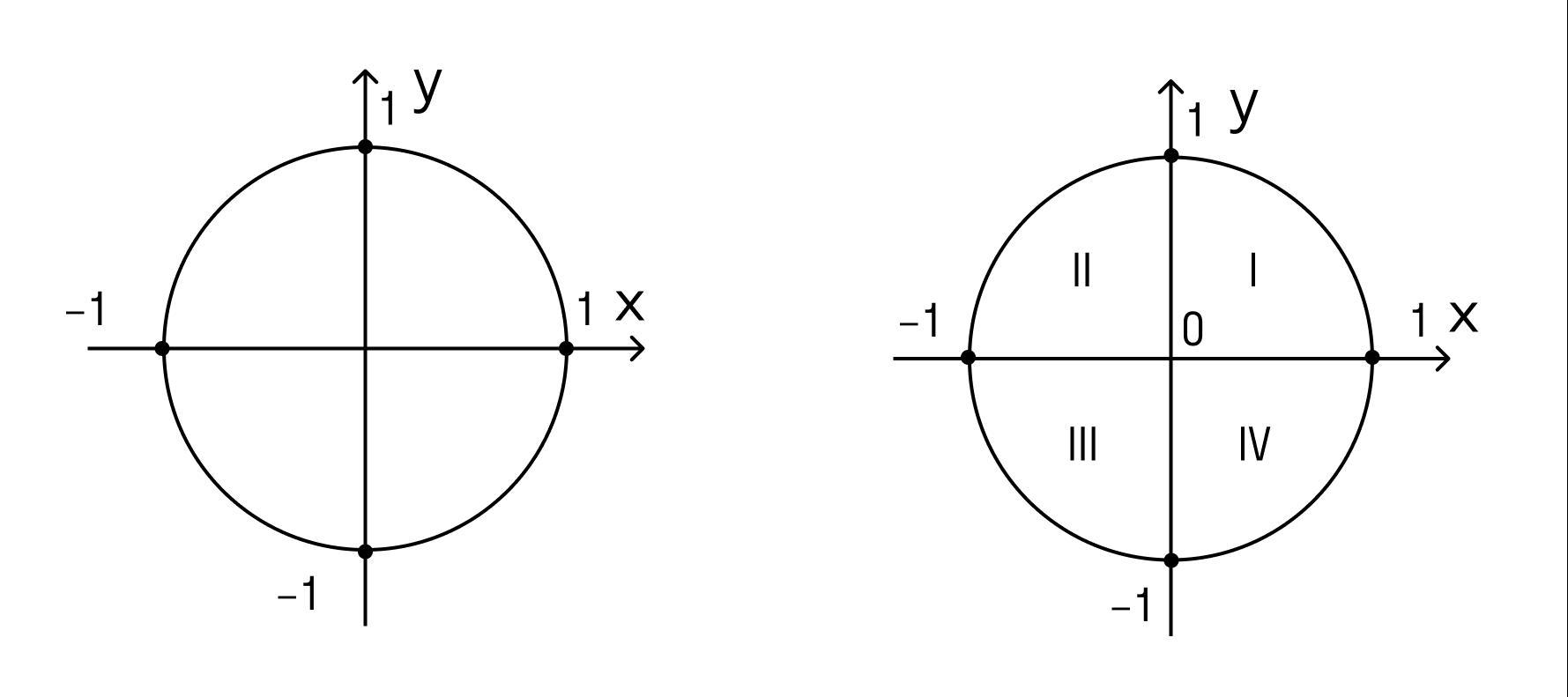
по условию угол альфа меньше пи и больше пи/2 (можно радианы перевести в градусы, если вам удобно: пи= 180, пи/2=90), то есть угол лежит во второй четверти (посмотрите на фото)
вспомним, что cos=x, a sin=y
во второй четверти у положителен, то есть синус тоже положителен, а х отрицателен, то есть косинус тоже отрицателен, значит
теперь найдем тангенс и котангенс
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sandrasergeevnadeput
Предмет: Химия,
автор: sokolovskaanastasia3
Предмет: Українська література,
автор: valeriecherneva
Предмет: География,
автор: babynoname
Предмет: Математика,
автор: savarovsky07