Предмет: Алгебра,
автор: ulaynkad213
Помогите пожалуйста с алгеброй (нужно решить 1,3,6)
Приложения:
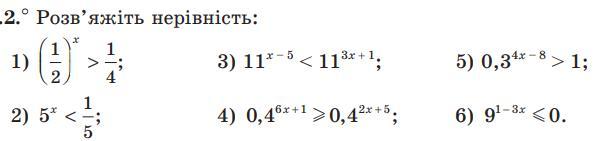
Ответы
Автор ответа:
1
Ответ:
Чтобы решить заданные показательные неравенства, надо привести показательные функции к одному основанию .
В данном примере функция убывающая, так как , поэтому
знак между аргументами противоположен знаку между функциями .
В данном примере функция возрастающая, так как , поэтому
знак между аргументами такой же, как и знак между функциями .
Все показательные функции, не зависимо от их основания, принимают только строго положительные значения . Поэтому показательная функция не может быть меньше 0 или равной 0 .
ulaynkad213:
вы мой спаситель
Похожие вопросы
Предмет: Українська мова,
автор: kostyaslobodyanik0
Предмет: Алгебра,
автор: ghbvvhh
Предмет: Английский язык,
автор: pobedaviktoria2022
Предмет: Математика,
автор: xstpd
Предмет: Геометрия,
автор: katyakapavl