Question

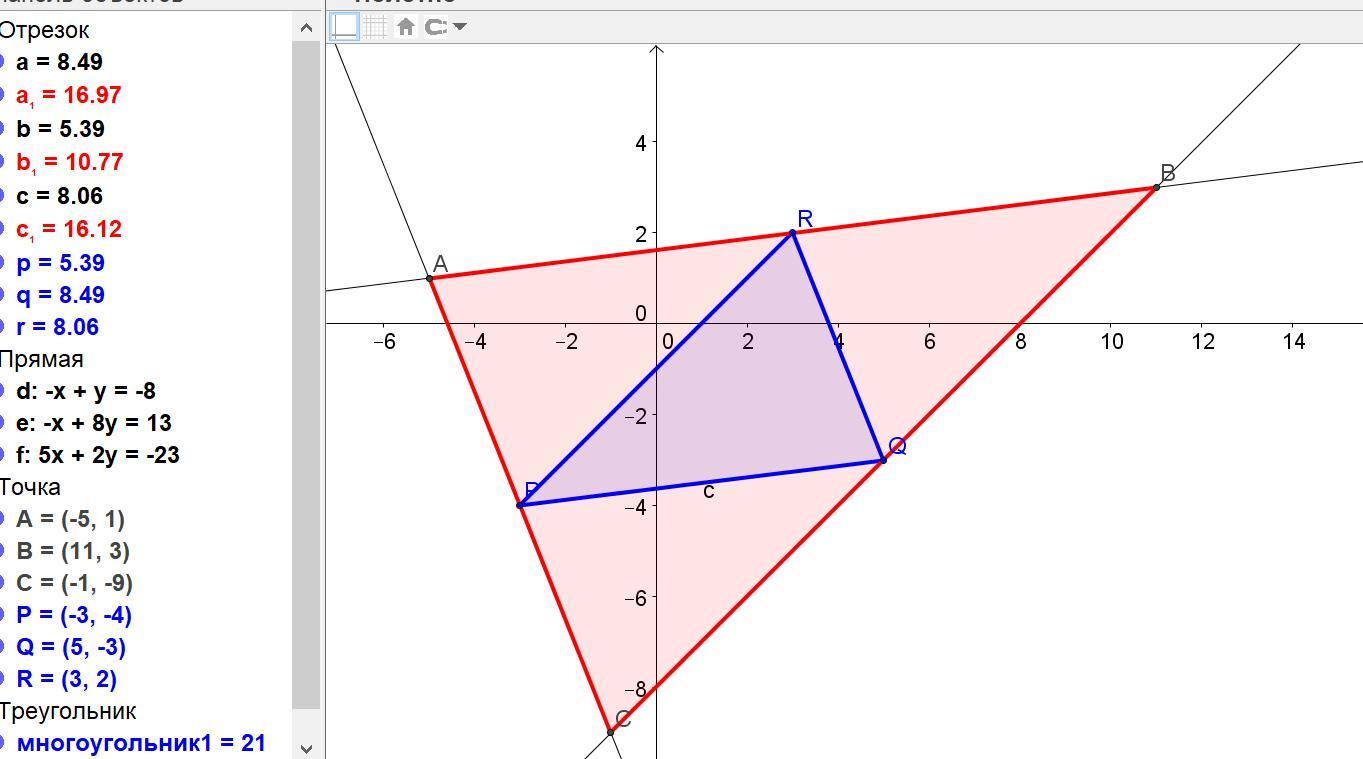
Даны середины сторон треугольника P(—3;-4),Q(5;-3), R(3;2). Найти уравнение его сторон.

Answer 1

Ответ:

АВ: х-8у+13=0; ВС: х-у-8=0; АС: 5х+2у+23=0.

Объяснение:

а) так как данные точки являются серединами сторон, то отрезки PQ, QR, PR - средние линии треугольника (см. небольшой чертёж во вложении);

б) по каждой паре предоставленных точек можно составить уравнения для каждой средней линии, потом по ней составить уравнение параллельной линии, содержащую третью точку. Этой же прямой будут принадлежать две вершины треугольника АВС.

PS. проверка арифметики не проводилась.

Answer 2

Даны середины сторон треугольника

P(-3;-4), Q(5;-3), R(3;2). Найти уравнение его сторон.

Находим векторы.

PQ = (5-(-3); -3-(-4)) = (8; 1).

QR = = (3-5); 2-(-3)) = (-2; 5).

PR = = (3-(-3)); 2-(-4)) = (6; 6).

Сторона АВ параллельна PQ и проходит через точку R, то есть направляющий вектор равен (8; 1).

Подставим в уравнение координаты точки R(3; 2).

Уравнение АВ: (x - 3)/8 = (y - 2)/1,

                           x - 3 = 8y – 16,

                          x - 8y + 13 = 0.

Аналогично находим уравнения других сторон.

Сторона ВС параллельна PR и проходит через точку Q, то есть направляющий вектор равен (6; 6).

Подставим в уравнение координаты точки Q(5; -3).

Уравнение ВC: (x - 5)/6 = (y + 3)/6,

                           x - 5 = y + 3,

                           x - y - 8 = 0.

Сторона AС параллельна QR и проходит через точку Р, то есть направляющий вектор равен (-2; 5).

Подставим в уравнение координаты точки P(-3;-4).

Уравнение АC: (x + 3)/(-2) = (y + 4)/5,

                          5x + 15 = -2y - 8,

                           5x + 2y + 23 = 0.