Question

3. У правильній трикутній призмі сторона основи дорівнює 2$\sqrt{3}$ см. Через сторону нижньої основи і протилежну вершину верхньої основи проведено площину, що утворює з площиною основи кут 60. Знайдіть площу поверхні призми.
4. Через діагональ нижньої основи і вершину верхньої основи правильної чотирикутної призми проведено площину, яка перетинає дві суміжні грані призми по прямих, що утворюють між собою
кут α. Сторона основи дорівнює m. Обчисліть площу повної поверхні призми.

Answer 1

Ответ:

3. Площадь полной поверхности призмы равна  (54 + 6√3) см².

4. Площадь полной поверхности призмы равна $\displaystyle \bf 2\sqrt{2}m^2\sqrt{ctg^2\frac{\alpha }{2}-1}+2m^2$

Объяснение:

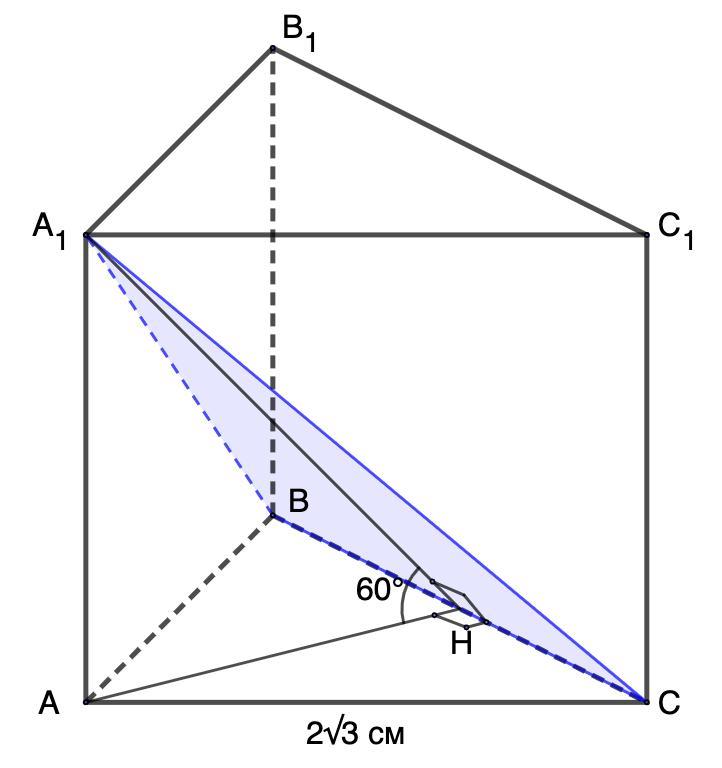
3. В правильной треугольной призме сторона основания равна 2√3 см. Через сторону нижнего основания и противоположную вершину верхнего основания проведена плоскость, образующая с плоскостью основания угол 60°. Найдите площадь поверхности призмы.

4. Через диагональ нижнего основания и вершину верхнего основания правильной четырехугольной призмы проведена плоскость, которая пересекает две смежные грани призмы по прямым, образующих между собой угол α. Сторона основания равна m. Вычислите площадь полной поверхности призмы.

3. Дано: АВСА₁В₁С₁ - правильная призма;

АС = 2√3 см;

Угол между ВА₁С и АВС равен 60°.

Найти: Sполн.

Решение:

• Основания правильной треугольной призмы - правильные треугольники, боковые грани - равные прямоугольники.

Проведем АН ⊥ ВС, соединим Н и А₁.

⇒ АН - проекция А₁Н.

• Прямая, проведённая в плоскости через основание наклонной, перпендикулярная к её проекции на эту плоскость, перпендикулярна и самой наклонной.

⇒ А₁Н ⊥ ВС.

• Угол между плоскостями - угол между перпендикулярами, проведенными к линии пересечения.

⇒ ∠А₁НА = 60°

1. Рассмотрим ΔАВС - равносторонний.

⇒ АН - высота, медиана.

НС = 2√3 : 2 = √3 (см)

По теореме Пифагора:

АН² = 12 - 3 = 9   ⇒   АН = 3 (см)

2. Рассмотрим ΔАА₁Н - прямоугольный.

$\displaystyle \bf \frac{AA_1}{AH}=tg 60^0\\\\AA_1=3\cdot\sqrt{3}$ (см)

3. Площадь полной поверхности призмы равна:

Sполн = Sбок + 2S осн

Sбок = Росн · Н, где Н - высота призмы.

Росн = 6√3 см   ⇒  Sбок = 6√3 · 3√3 = 54 (см²)

$\displaystyle \bf S_{OCH}=\frac{a^2\sqrt{3} }{4}=\frac{12\sqrt{3} }{4}=3\sqrt{3}$  (см²)

Sполн = (54 + 6√3) см²

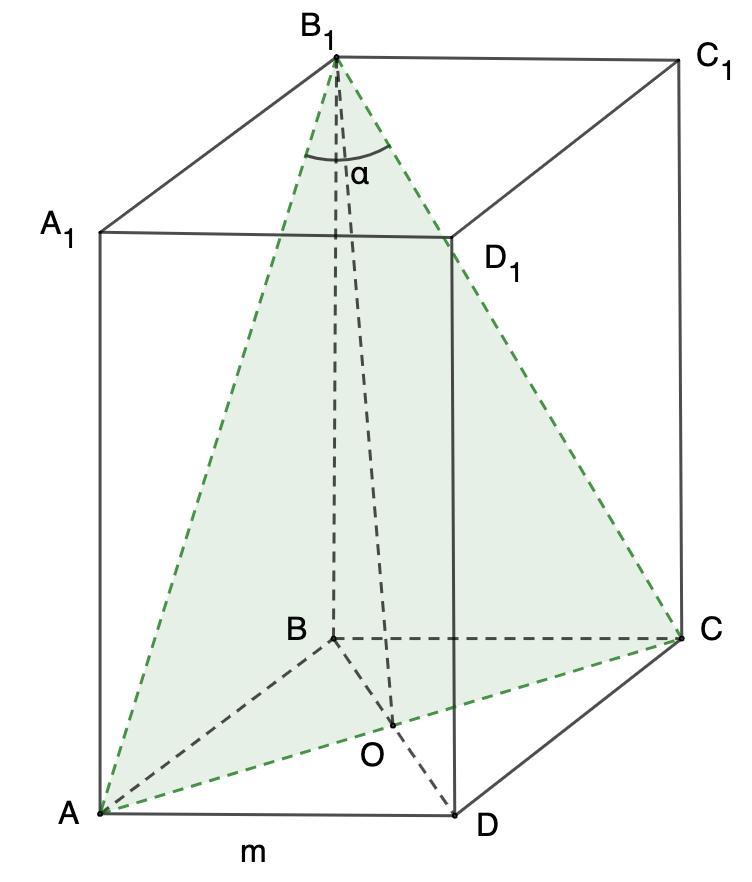
4. Дано: ABCDA₁B₁C₁D₁ - правильная призма.

AD = m;  ∠AB₁C = α

Найти: Sполн

Решение:

ABCD - квадрат

⇒ Росн = 4m, Sосн = m²

Найдем высоту ВВ₁.

1. Рассмотрим ΔACD - прямоугольный.

По теореме Пифагора:

АС = m√2

2. Рассмотрим ΔАВ₁С - равнобедренный.

• В квадрате диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.

⇒ АС ⊥ ОВ

Тогда по теореме о трех перпендикулярах

ОВ₁ ⊥ АС

⇒ В₁О - высота, медиана, биссектриса.

⇒ ∠АВ₁О = α/2, АО = (m√2)/2

$\displaystyle \bf \frac{B_1O}{AO}=ctg\frac{\alpha }{2} \\\\B_1O=\frac{m\sqrt{2} }{2} \cdot{ctg\frac{\alpha }{2} }$

3. Рассмотрим ΔВВ₁О - прямоугольный.

$\displaystyle \bf B_1O=\frac{m\sqrt{2} \;ctg\frac{\alpha }{2} }{2};\;\;\;\;\;OB=\frac{m\sqrt{2} }{2}$

По теореме Пифагора:

$\displaystyle \bf BB_1^2=\frac{m^2\cdot2\;ctg^2\frac{\alpha }{2} }{4} -\frac{m^2\cdot2}{4}=\frac{m^2\;ctg^2\frac{\alpha }{2} }{2} -\frac{m^2}{2}=\frac{m^2}{2}(ctg^2\frac{\alpha }{2}-1)$

$\displaystyle \bf BB_1=\sqrt{\frac{m^2}{2}(ctg^2\frac{\alpha }{2}-1)} =\frac{m\sqrt{2} }{2}\sqrt{ctg^2\frac{\alpha }{2}-1}$

Sбок = Росн · ВВ₁=

$\displaystyle \bf =\frac{4m^2\sqrt{2} }{2}\sqrt{ctg^2\frac{\alpha }{2}-1}=2\sqrt{2}m^2\sqrt{ctg^2\frac{\alpha }{2}-1}$

Sполн = Sбок + 2S осн=    

 $\displaystyle \bf =2\sqrt{2}m^2\sqrt{ctg^2\frac{\alpha }{2}-1}+2m^2$