Question

СРОЧНО задача 9 класс

Answer 1

Ответ:

АВ = 16 см;  АС = 24 см

Пошаговое объяснение:

Требуется найти АВ м АС.

Дано: ΔАВС;

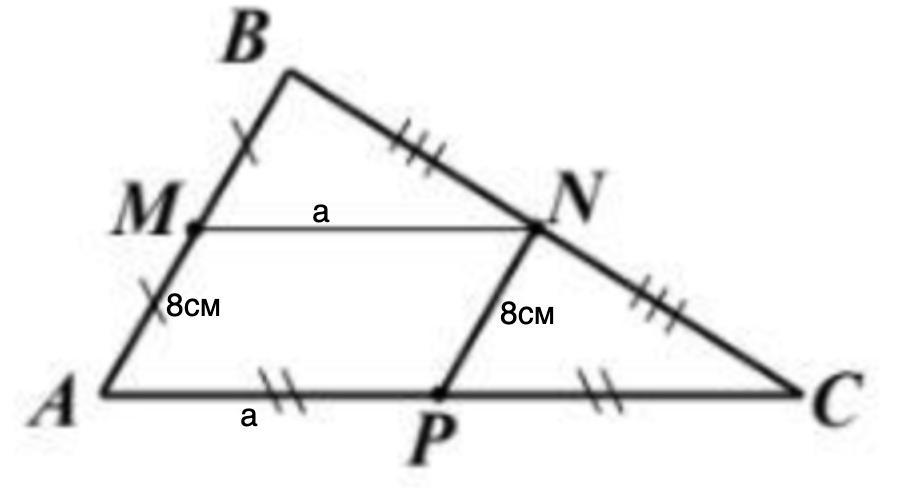
MN и NP - средние линии;

PN = 8 см; P(AMNP) = 40 см.

Найти: АВ и АС.

Решение:

Рассмотрим ΔАВС.

MN и NP - средние линии.

• Средняя линия треугольника параллельна стороне, которую не пересекает.

⇒ NP || AB; MN || AС.

Рассмотрим AMNP.

NP || AМ; MN || AP

⇒ AMNP - параллелограмм (по определению)

• Противоположные стороны параллелограмма равны.

⇒АМ = NP = 8 см.

• Периметр параллелограмма равен удвоенной сумме смежных сторон.

Пусть АР = MN = а см;

Тогда периметр равен:

Р(AMNP) = 2 · (АР + АМ)

40 = 2 · (а + 8)

2а = 40 - 16   |:2

a = 12

⇒ АР = MN = 12 см.

• Средняя линия равна половине длины стороны, которую она не пересекает.

⇒ АВ = NP · 2 = 16 см

АС = MN · 2 = 24 см