Question

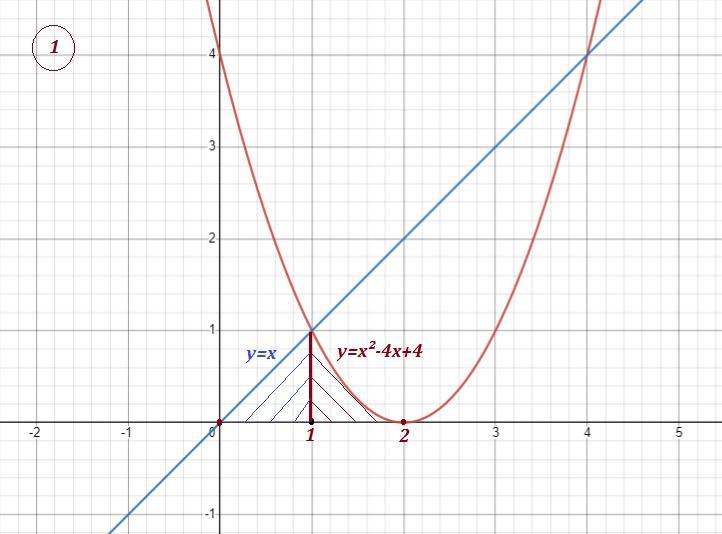
Вычислите площадь фигуры, ограниченной на отрезках [a; b] и [b; c], соответственно, графиками функций f(x) и g(x) и осью Ox.

f(x)=x, [0;1] и g(x)=x^2-4x+4, [1;2]

f(x)=x^2+4x+4, [-2; - 1] и g(x)=-x, [-1; 0]​

Answer 1

Ответ:

Нарисуем заданные области. Обе области состоят из двух областей, площади которых надо сложить . Площади областей находим с помощью определённого интеграла .

$\displaystyle 1)\ \ f(x)=x\ ,\ x\in [\, 0;1\, ]\ \ \ ,\ \ \ g(x)=x^2-4x+4\ ,\ x\in [\, 1;2\, ]\\\\S=\int\limits_0^1\, x\, dx+\int\limits_1^2\, (x^2-4x+4)\, dx=\frac{x^2}{2}\, \Big|_0^1+ \int\limits_1^2\, (x-2)^2\, dx=\\\\\\=\frac{1}{2}+\frac{(x-2)^3}{3}\, \Big|_1^2=\frac{1}{2}+\Big(0-\frac{-1}{3}\Big)=\frac{1}{2}+\frac{1}{3}=\bf \frac{5}{6}$        

$\displaystyle 2)\ \ f(x)=x^2+4x+4\ ,\ x\in [\, -2\, ;-1\, ]\ \ \ ,\ \ \ g(x)=-x\ ,\ x\in [\, -1;\ 0\, ]\\\\S=\int\limits_{-2}^{-1}\, (x^2+4x+4)\, dx+\int\limits_{-1}^0\, (-x)\, dx= \int\limits_{-2}^{-1}\, (x+2)^2\, dx-\frac{x^2}{2}\, \Big|_{-1}^0=\\\\\\=\frac{(x+2)^3}{3}\, \Big|_{-2}^{-1}-\Big(0-\frac{1}{2}\Big)=\Big(\frac{1}{3}-0\Big)+\frac{1}{2}=\frac{1}{3}+\frac{1}{2}=\bf \frac{5}{6}$