Question

Геометрия даю 100 баллов!​

Answer 1

Ответ:

2. Радиус правильного треугольника равен 4√6 см.

3. Длина дуги равна 21,98 см.

Площадь сектора равна 165 см².

4. Точка В(-4;-1) перейдет  в точку  В₁(2; -3) при этом же параллельном переносе.

Объяснение:

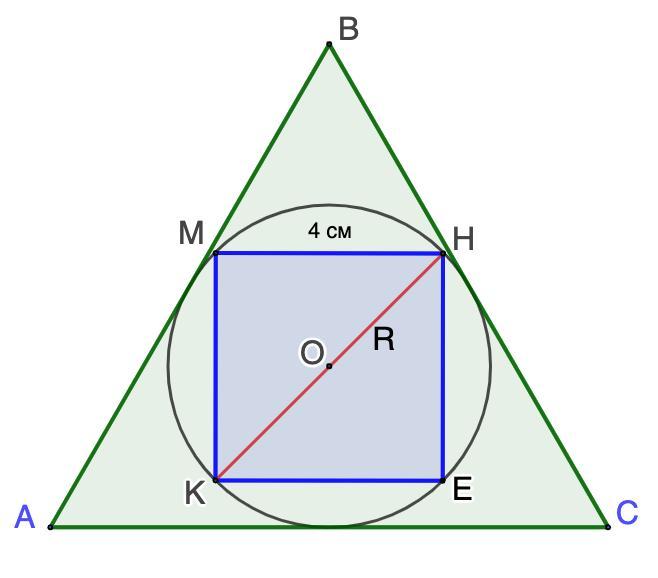
2. Дано: Окр.О;

КМНЕ - квадрат, вписанный в Окр.О;

ΔАВС - равносторонний, описан около Окр.О.

МН = 4 см.

Найти: АВ.

Решение:

• Диаметр окружности - диагональ вписанного квадрата.

Рассмотрим ΔКМН - прямоугольный.

По теореме Пифагора:

$\displaystyle \bf KH=\sqrt{KM^2+MH^2}=\sqrt{16+16}=4\sqrt{2}\;_{(CM)}$

⇒ R = 4√2 : 2 = 2√2 (см)

Рассмотрим ΔАВС - равносторонний.

Радиус вписанной окружности в равносторонний треугольник равен:

$\displaystyle \bf R=\frac{a}{2\sqrt{3} } \;\;\;\Rightarrow \;\;a=2\sqrt{3}R$  ,  где а - сторона треугольника.

АВ = 2√3 · 2√2 = 4√6 (см)

Радиус правильного треугольника равен 4√6 см.

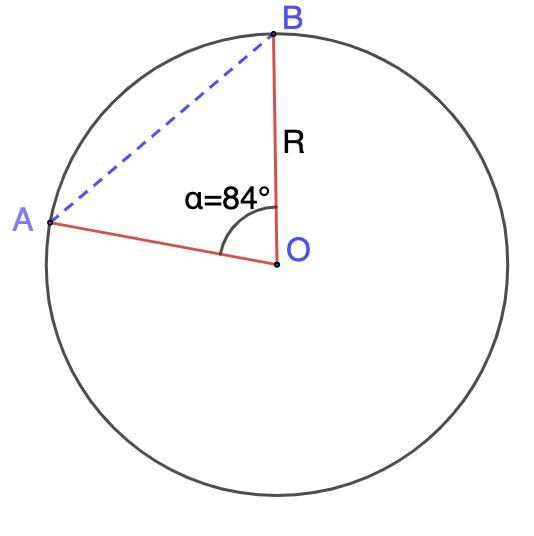
3. Дано: Окр.О;

∠AOB = α = 84° - центральный;

L = 30π см - длина окружности;

Найти: L ◡AB;  Sсект.

Решение:

Длина дуги:

$\displaystyle \bf L(\smile AB)=\frac{\pi R}{180^0}\cdot{\alpha }$

L = 2πR = 30π  (см) ⇒ R = 15 см

$\displaystyle \bf L(\smile AB)=\frac{\pi \cdot15}{180^0}\cdot84^0=7\pi =21,98\;_{(CM)}$

Длина дуги равна 21,98 см.

Площадь сектора:

$\displaystyle \bf S_{CEKT}=\frac{\pi R^2}{360^0}\cdot{\alpha }$

$\displaystyle \bf S_{CEKT}=\frac{\pi\cdot225^0}{360^0}\cdot{84^0 }=52,5\pi \approx 165\;_{(CM^2)}$

Площадь сектора равна 165 см².

4. Точка А (-3; 4) при параллельном переносе отображаемся в точку А₁(3; 2). В какую точку перейдет точка В(-4;-1) при этом же параллельном переносе.

Параллельный перенос задается формулой:

$\displaystyle \bf x'=x+a;\;\;\;\;\;y'=y+b$

Найдем a и b:

А (-3; 4) → А₁(3; 2)

3 = -3 + а ⇒ а = 6;

2 = 4 + b ⇒ b = -2

В(-4;-1)

Найдем координаты искомой точки:

$\displaystyle \bf x'=-4+6=2;\;\;\;\;\;y'=-1-2=-3$

⇒  В₁(2; -3)

Точка В(-4;-1) перейдет  в точку  В₁(2; -3) при этом же параллельном переносе.