Question

Алгебра даю 100 баллов!​

Answer 1

Ответ:

6)  Геометрическая прогрессия   $a_1=27\ ,\ a_3=3$  .

Применим свойство  $\bf a_{n}^2=a_{n-1}\cdot a_{n+1}$  .

$a_2^2=a_1\cdot a_3=27\cdot 3=81\ \ ,\ \ a_2=\pm 9$  

Так как члены геом. прогрессии по условию положительны, то выбираем   $a_2=9$  .

$\boldsymbol{q}=\dfrac{a_2}{a_1}=\dfrac{9}{27}=\bf \dfrac{1}{3}$    

Сума первых шести членов геометрической прогрессии:

$S_6=\dfrac{b_1(1-q^6)}{1-q}=\dfrac{27\, \Big(1-\dfrac{1}{3^6}\Big)}{1-\dfrac{1}{3}}=\dfrac{3^3\cdot \dfrac{3^6-1}{3^6}}{\dfrac{3-1}{3}}=\dfrac{3^6-1}{3^3\cdot \dfrac{2}{3}}=\dfrac{3^6-1}{3^2\cdot 2}=\dfrac{728}{18}\ ,\\\\\bf S_6=40\dfrac{4}{9}$

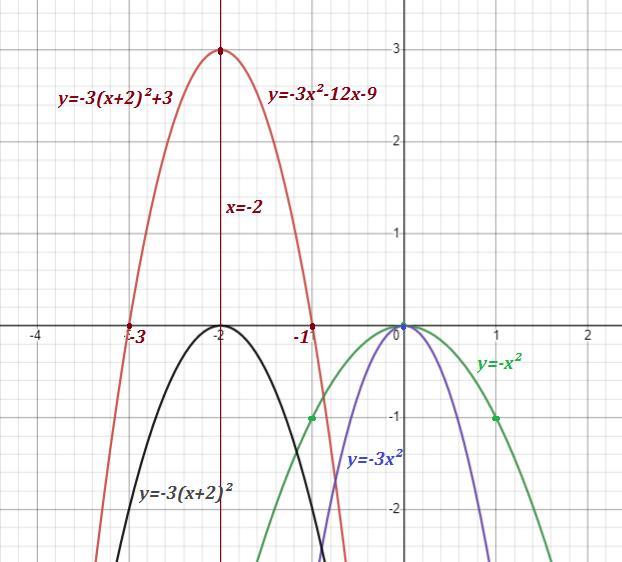
7) График функции   $y=-3x^2-12x-9$  .

$-3x^2-12x-9=-3(x^2+4x)-9=-3\cdot \Big((x+2)^2-4\Big)-9=\\\\=-3\cdot (x+2)^2+12-9=\bf -3\, (x+2)^2+3$  

Вершина параболы в точке (-2 ; 3 ) , ось симметрии  х= -2 , ветви направлены вниз . Можно нарисовать сначала параболу  $y=-x^2$  , затем сжать в 3 раза к оси ОУ , потом сдвинуть её на 2 единицы влево вдоль ОХ , а потом вверх вдоль оси ОУ на 3 единицы .

Промежутки знакопостоянства:

$\bf y > 0$  при   $\boldsymbol{x\in (-3\ ;-1\ )}$   ;  

$\bf y < 0$  при   $\boldsymbol{x\in (-\infty \, ;-3\ )\cup (-1\ ;+\infty \, )}$