Предмет: Алгебра,
автор: frog7895
РЕШИТЕ ПОЖАЛУЙСТА !!!(МНОГО БАЛОВ ЗА ОТВЕТ)
Приложения:

Ответы
Автор ответа:
1
Ответ:
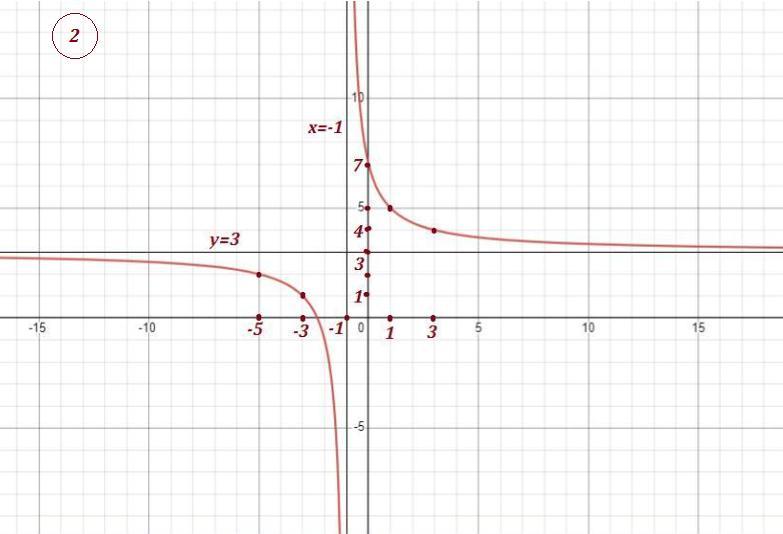
2) Привести функцию к виду
.
Гипербола имеет асимптоты у=3 и х= -1 ., проходит через точки
(0:7) , (1:5) , (3:4) , (-3:1) , (-5,2) .
3) Составить сложные функции .
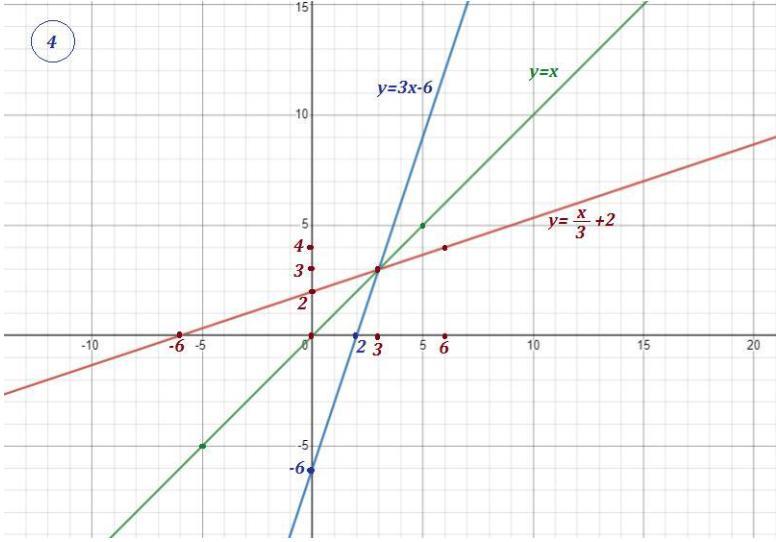
4) а) Найти обратную функцию для . Она проходит через точки (0;-6) , (2;0) .
Выразим переменную х через у .
Теперь изменим обозначения: вместо х напишем у , а вместо у напишем х . Получим запись обратной функции.
Эта прямая проходит через точки (0;2) , (-6;0) .
б) Графики заданной функции и обратной функции будут симметричны прямой у=х (биссектрисы 1 и 3 координатных углов) .
Приложения:
frog7895:
БОЖЕ СПАСИБО!!!
а картинки, к каким заданиям относятся?
yна картинке к 4 заданию стоит номкр 4 в верхнем левом углу
а на 1 фотографии?
написано 2 , в ответе написано, что это гипербола, не можешь её от прямой отличить ?
зачем вы вопросы задаёте? для вас ответы всё равно бесполезны, разве что списать ...
не заметил сразу, сори.
Похожие вопросы
Предмет: Английский язык,
автор: 0660068941dan
Предмет: Химия,
автор: vanberezhnoy
Предмет: Биология,
автор: Ghic98
Предмет: История,
автор: Аноним
Предмет: Алгебра,
автор: Vasilisa170506