Предмет: Алгебра,
автор: tdubiraliev
Решите систему пожалуйста, это не линейное уравнение с 2 переменными, можете объяснить
Приложения:
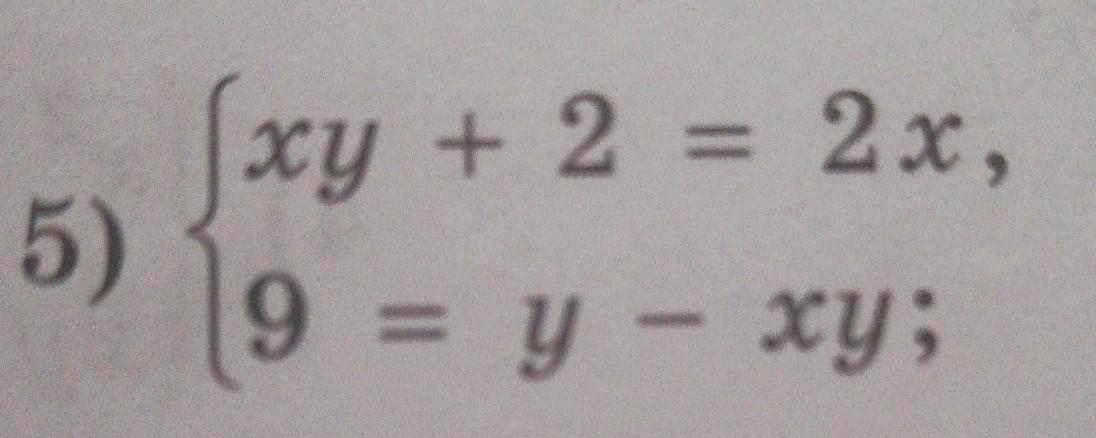
Ответы
Автор ответа:
1
Ответ:
1-x≠0 (потому что знаменатель не может быть равен 0)
x≠1
Чтобы произведение было равно 0, то числитель должен быть равен 0.
a=2, b=5, c=2
D=b²-4ac
D=25-16=9
tdubiraliev:
спасибо большое!
Похожие вопросы
Предмет: Химия,
автор: kusbekovagulaim
Предмет: Физика,
автор: annet64
Предмет: Химия,
автор: madihan91
Предмет: Алгебра,
автор: egor964909
Предмет: Русский язык,
автор: anny1727