Предмет: Алгебра,
автор: kovalchuktymur221
Довести нерівність, срочно!! плачу любые деньги
Приложения:
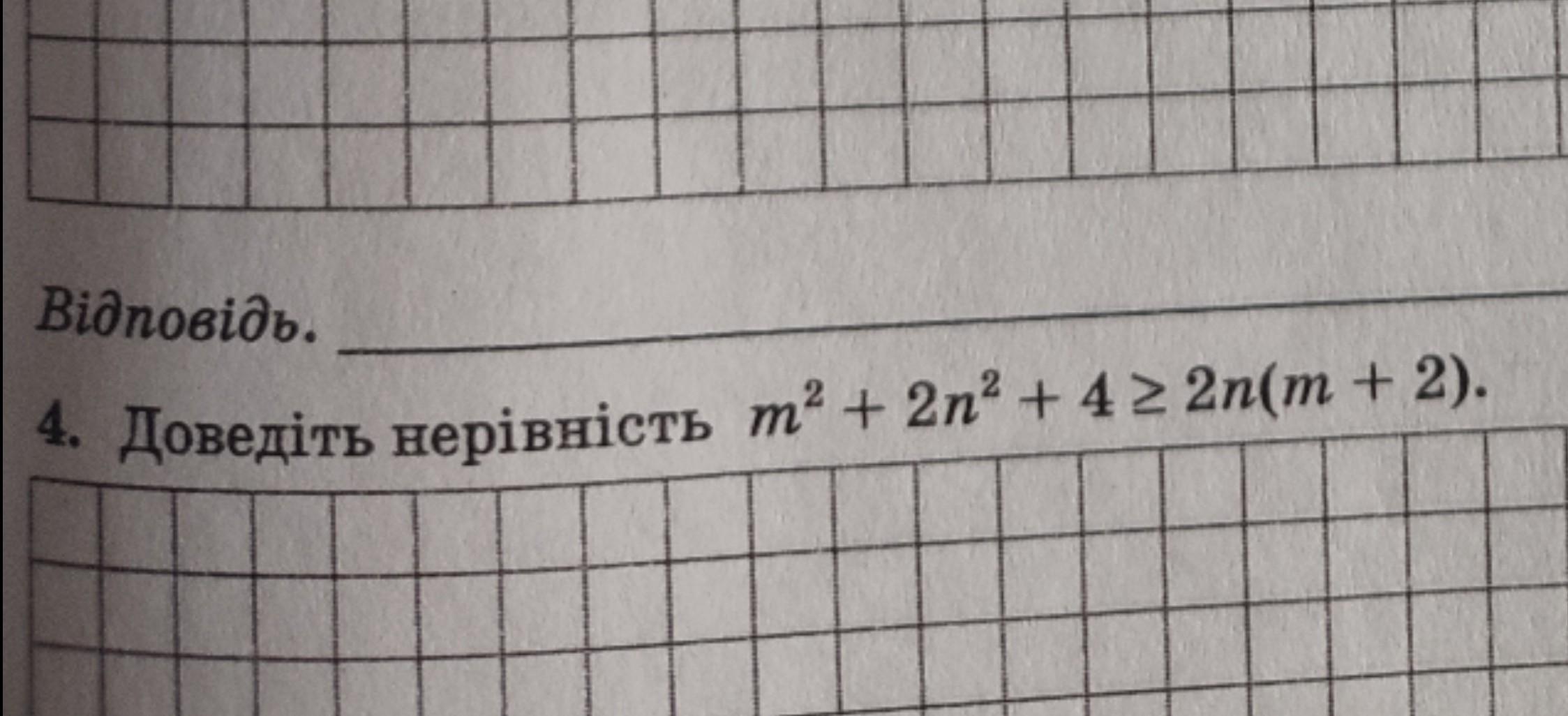
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
4 . m² + 2n² + 4 ≥ 2n( m + 2 ) .
Cкладемо різницю лівої і правої частин нерівності і спростимо :
m² + 2n² + 4 - 2n( m + 2 ) = m² + 2n² + 4 - 2nm - 4n = ( m² - 2mn + n² ) +
+ ( n² - 4n + 4 ) = ( m - n )² + ( n - 2 )² ≥ 0 як сума двох квадратів .
Отже , дана нерівність правильна при будь - яких значеннях m i n .
kovalchuktymur221:
от души братик
Похожие вопросы
Предмет: Қазақ тiлi,
автор: azhgalievv
Предмет: История,
автор: eleusizalina2010
Предмет: Математика,
автор: anastasiaostapcuk16
Предмет: История,
автор: IdIck
Предмет: Русский язык,
автор: Аноним