Предмет: Математика,
автор: dalexandr127
Помогите, даю 100 баллов
Приложения:
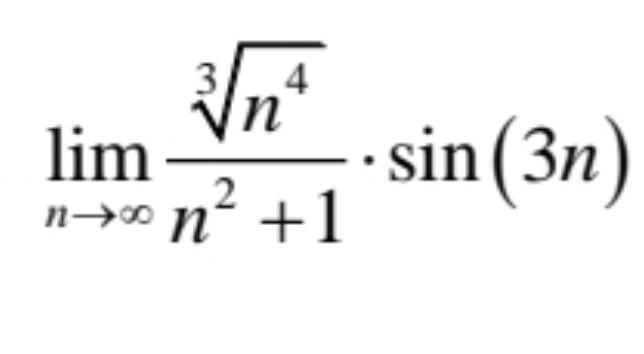
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
Так как при функция
бесконечно малая, а функция
ограничена, то справедливо, что
- бесконечно малая при
.
Тогда верно, что:
Задание выполнено!
Похожие вопросы
Предмет: Українська мова,
автор: bogdan5410
Предмет: Українська мова,
автор: kolyamelnyk12
Предмет: Русский язык,
автор: sdauletbek7
Предмет: Русский язык,
автор: mukhammad12
Предмет: Геометрия,
автор: elizabetpiu205