Question

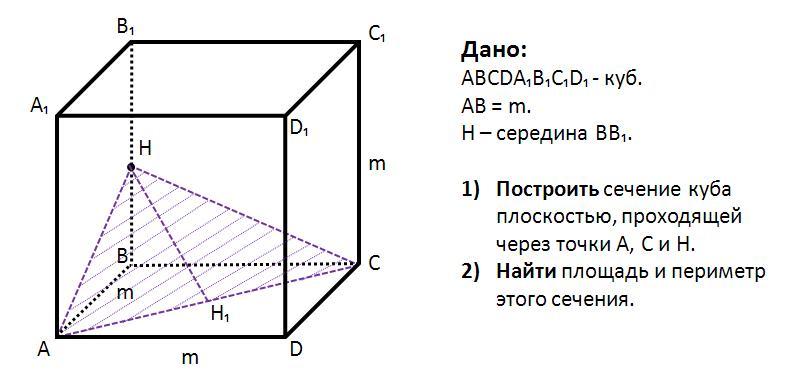
Побудуйте переріз куба АВСDA1B1C1D1 площиною, що проходить через вершини A, C і середину ребра BB1. Знайдіть периметр і площу перерізу, якщо AB = m.

Answer 1

Ответ:

Площадь S сечения куба равна (m²√6)/4 единиц квадратных.

Периметр Р сечения куба равен m(√2+√5).

Объяснение:

Часть 1. Построение сечения куба.

• Аксиома стереометрии: через любые 3 точки, не лежащие на 1 прямой, можно провести плоскость и при том только одну.

Мы имеем 3 точки, не лежащие на одной прямой: А, С и Н - середина ВВ₁, значит, по вышеуказанной аксиоме стереометрии, через эти три точки мы можем провести плоскость и при этом только одну. Определим, по каким отрезкам плоскость (АСН) будет пересекать плоскости граней куба.

1) А ∈ (АВС), С ∈ (АВС) ⇒ (АСН) ∩ (АВС) = АС.

2) А ∈ (АВВ₁), Н ∈ (АВВ₁) ⇒ (АСН) ∩ (АВВ₁) = АН.

3) С ∈ (ВСС₁), Н ∈ (ВСС₁) ⇒ (АСН) ∩ (ВСС₁) = СН.

Проводим прямые АС, СН и АН. Плоскость, заключённая внутри этих прямых, является искомой секущей плоскостью куба.

АС ∈ (АСН), АН ∈ (АСН), СН ∈ (АСН) ⇒ (АСН) - искомое сечение куба.

Часть 2. Нахождение площади и периметра сечения куба.

Сечение куба - треугольник. Площадь произвольного треугольника мы можем найти по формуле S = 1/2*a*hₐ, где а - сторона треугольника, hₐ - высота, проведённая к этой стороне.

Проведём HH₁ ⊥ AC.

HH₁ ⊥ AC ⇒ HH₁ высота ΔАСН. Тогда площадь ΔАСН мы можем найти следующим образом:

S = 1/2 * AC * HH₁

• Грани куба - квадраты.

АВСDA₁B₁C₁D₁ - куб ⇒ АВСD - квадрат.

• Диагональ квадрата равна стороне квадрата, умноженной на корень из двух.

АВСD - квадрат, АС - диагональ ⇒ АС = АВ*√2 = m√2

• Все рёбра куба равны между собой.

АВСDA₁B₁C₁D₁ - куб ⇒ АВ = ВС = ВВ₁.

Н - середина ВВ₁, тогда НВ = 1/2*ВВ₁ = 1/2m.

Рассмотрим ΔНВС - прямоугольный (∠НВС = 90°).

По теореме Пифагора НС² = НВ²+ВС².

$\displaystyle \bf HC = \sqrt{HB^2+BC^2} =\sqrt{\Big(\frac{1}{2}m\Big)^2+m^2 } = \sqrt{1\frac{1}{4}m^2 }=\sqrt{\frac{5}{4}m^2 }$

• Признак равенства прямоугольных треугольников: если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны

ΔАВН и ΔНВС - прямоугольные (т.к. ∠НВА=∠НВС=90°), АВ=ВС (т.к. фигура - куб), НВ - общая сторона ⇒ ΔНВА=ΔНВС.

Из равенства треугольников ΔНВА и ΔНВС имеем АН=НС=√(5/4m²).  

Рассмотрим ΔАНС - равнобедренный (АН=НС).

• В равнобедренном треугольнике высота, проведенная к основанию, является и медианой, и биссектрисой.

ΔАНС - равнобедренный, НН₁ - высота ⇒ НН₁ - медиана и биссектриса.

Так как НН₁ - медиана, АН₁=Н₁С = 1/2*АС = 1*2*m√2 = (m√2)/2

Рассмотрим ΔНН₁С - прямоугольный (∠НН₁С = 90°).

По теореме Пифагора НС² = Н₁С²+НН₁², отсюда:

$\displaystyle \bf HH_1=\sqrt{HC^2-H_1C^2} = \sqrt{\Big(\sqrt{1\frac{1}{4}m^2 }\Big)^2-\Big(\frac{m\sqrt{2} }{2}\Big)^2 } = \sqrt{\frac{5m^2}{4}-\frac{2m^2}{4} }=\\\\ =\sqrt{\frac{5m^2-2m^2}{4} }=\sqrt{\frac{3m^2}{4} } =\frac{m\sqrt{3} }{2}$

Мы имеем НН₁ и АС. Подставляем в формулу нахождения площади нашего треугольника:

$\bf \displaystyle S_{AHC}=\frac{1}{2}\cdot AC\cdot HH_1 = \frac{1}{2}\cdot m\sqrt{2} \cdot\frac{m\sqrt{3} }{2} =\frac{m^2\sqrt{6} }{4}$

Площадь S сечения куба равна (m²√6)/4 единиц квадратных.

• Периметр треугольника равен сумме трёх его сторон.

$\displaystyle \bf P_{ACH} = AC + HC+AH=\sqrt{\frac{5}{4}m^2 }+ \sqrt{\frac{5}{4}m^2 } +m\sqrt{2 }= 2\cdot \frac{m\sqrt{5} }{2} +m\sqrt{2}=\\\\ =m\sqrt{2}+m\sqrt{5}=m(\sqrt{2}+\sqrt{5})$

Периметр Р сечения куба равен m(√2+√5).

#SPJ1