Question

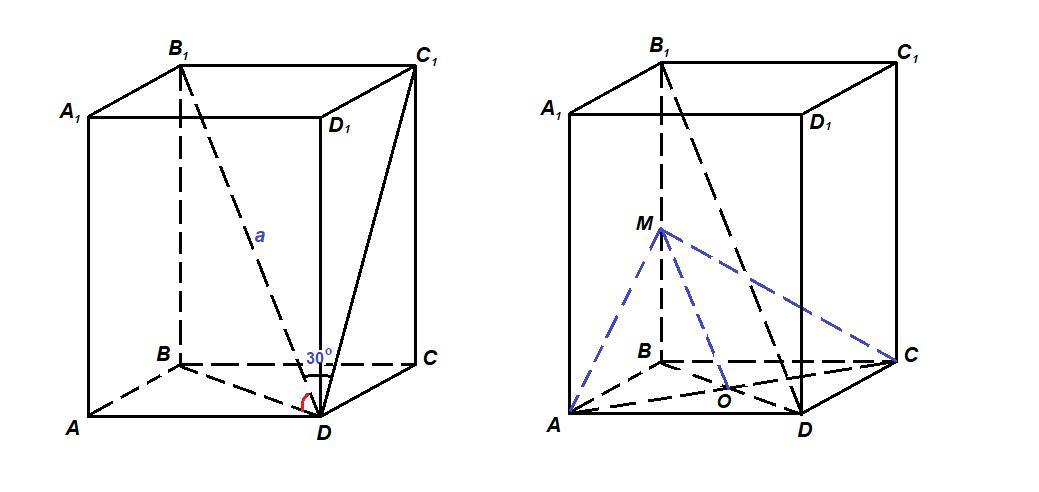
‼️‼️‼️‼️ ДАЮ 50 БАЛЛОВ ТОМУ КТО РЕШИТ‼️‼️‼️‼️‼️

Answer 1

Ответ:

1) Ребро основания равно 0,5а.

2) Угол между диагональю призмы и плоскостью основания равен 60°.

3) Площадь боковой поверхности призмы равна а²√3.

4) $S_{AMC}=\dfrac{a^2\sqrt{2}}{8}$

Объяснение:

Призма правильная, значит в основании лежит квадрат, а боковые грани - равные прямоугольники.

B₁D = a - диагональ призмы.

В₁С₁⊥C₁D₁ и B₁C₁⊥CC₁, значит В₁С₁⊥(СС₁D), тогда

С₁D - проекция диагонали B₁D на плоскость боковой грани, а

∠B₁DC₁ = 30° - угол между диагональю и плоскостью боковой грани.

1)

Рассмотрим ΔB₁C₁D:

∠B₁C₁D = 90°, так как В₁С₁⊥(СС₁D).

B₁C₁ = B₁D · sin 30° = a · 0,5 = 0,5a

Ребро основания равно 0,5а.

2)

BD - проекция B₁D на плоскость (АВС), значит

∠B₁DB - угол между диагональю B₁D и плоскостью основания - искомый.

Из прямоугольного треугольника B₁C₁D:

$CC_1=B_1D\cdot \cos 30^\circ=a\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}$

В любой призме боковые ребра равны:

$BB_1=CC_1-\dfrac{a\sqrt{3}}{2}$

Из прямоугольного треугольника BB₁D:

$\sin\angle B_1DB =\dfrac{BB_1}{B_1D}=\dfrac{a\sqrt{3}}{2}:a=\dfrac{\sqrt{3}}{2}$

∠B₁DB = 60°

3)

• Площадь боковой поверхности прямой призмы равна произведению периметра основания на боковое ребро.

$\boldsymbol{S}=P_{ABCD}\cdot BB_1=4\cdot 0,5a\cdot \dfrac{a\sqrt{3}}{2}=2a\cdot \dfrac{a\sqrt{3}}{2}\boldsymbol{=a^2\sqrt{3}}$

4)

Пусть М - середина ВВ₁, О - точка пересечения диагоналей, а, значит, середина BD.

Тогда ОМ - средняя линия треугольника B₁DB и ОМ║B₁D.

Тогда и плоскость АМС║B₁D по признаку параллельности прямой и плоскости.

АМС - сечение призмы плоскостью, которая проходит через диагональ основания (АС) и параллельна B₁D.

$AC=AB\sqrt{2}=0,5a\sqrt{2}=\dfrac{a\sqrt{2}}{2}$ как диагональ квадрата.

$MO=\dfrac{B_1D}{2}=\dfrac{a}{2}$  как средняя линия треугольника B₁DB.

ВО⊥АС по свойству диагоналей квадрата,

ВО - проекция МО на плоскость основания, значит

МО⊥АС по теореме о трех перпендикулярах.

Тогда МО - высота ΔАМС.

$S_{AMC}=\dfrac{1}{2}AC\cdot MO$

$\boldsymbol{S_{AMC}}=\dfrac{1}{2}\cdot \dfrac{a\sqrt{2}}{2}\cdot \dfrac{a}{2}\boldsymbol{=\dfrac{a^2\sqrt{2}}{8}}$