Question

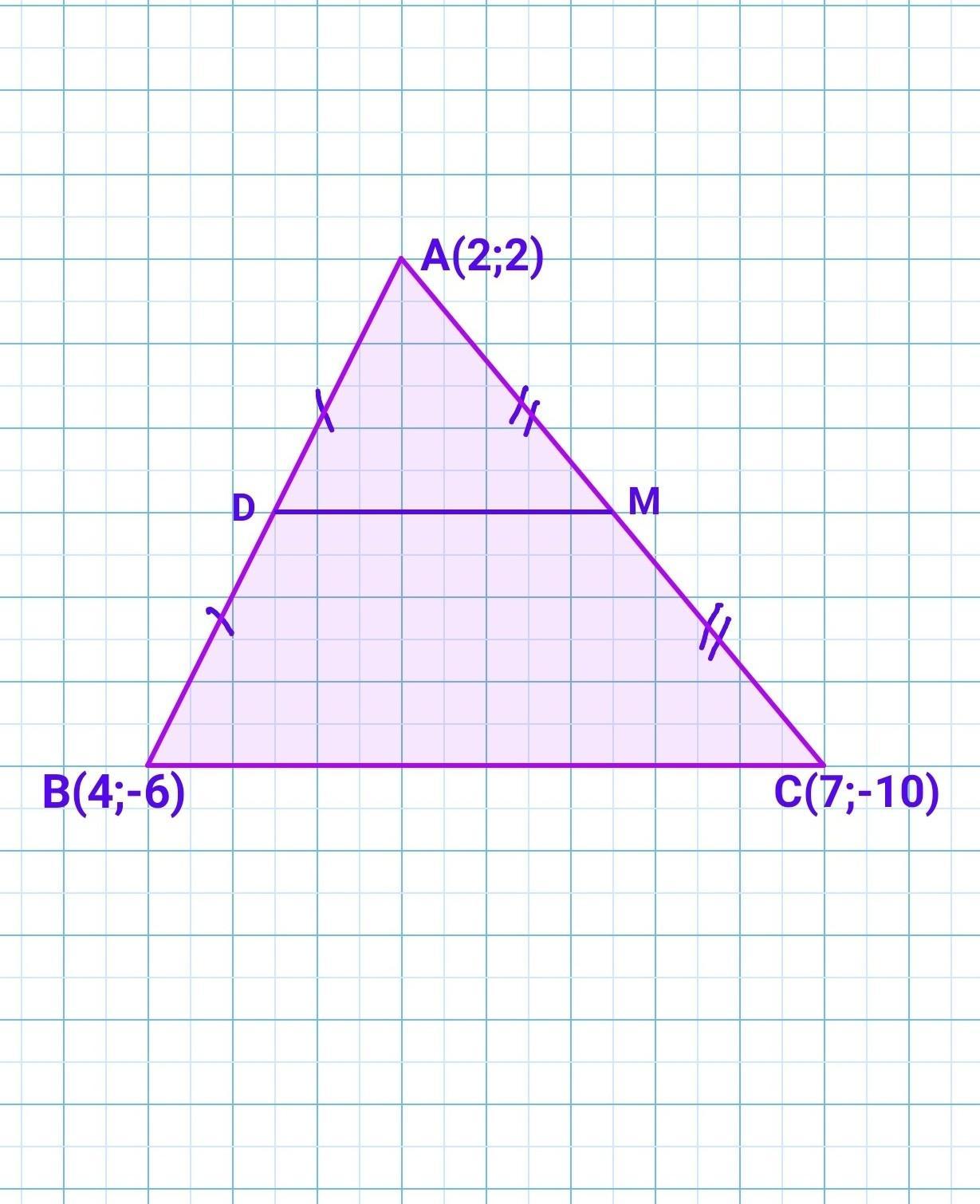
Знайти довжину середньої лінії ДМ трикутника АВС (ДМ ∥ ВС), якщо А(2;2), С(7;-10), В(4;-6). 2,5 6,5 2,6 7,3

Answer 1

Ответ:

DM=2,5

Объяснение:

Треба знайти довжину середньої лінії DМ трикутника АВС (ДМ II ВС), якщо А(2;2), С(7;-10), В(4;-6).

Відстань між двома точками $A(x_1;y_1) \: \: i \: \: B(x_2;y_2)$ знаходиться за формулою:

$\boxed {\bf AB = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} }$

Знайдемо довжину ВС:

$BC = \sqrt{ {(7 - 4)}^{2} + ( - 10 - ( - 6))^2 } = \sqrt{ {3}^{2} + {( - 4)}^{2} } = \\ \\ = \sqrt{9 + 16} = \sqrt{25} =\bf 5$

• Середньою лінією трикутника називають відрізок, який сполучає серединидвох його сторін.

Середня лінія трикутника, яка сполучає середини двох сторін, паралельна до третьої сторони і дорівнює ії половині, тому:

$DM = \dfrac{1}{2} BC = \dfrac{1}{2} \cdot5 = \bf 2,5$

#SPJ1