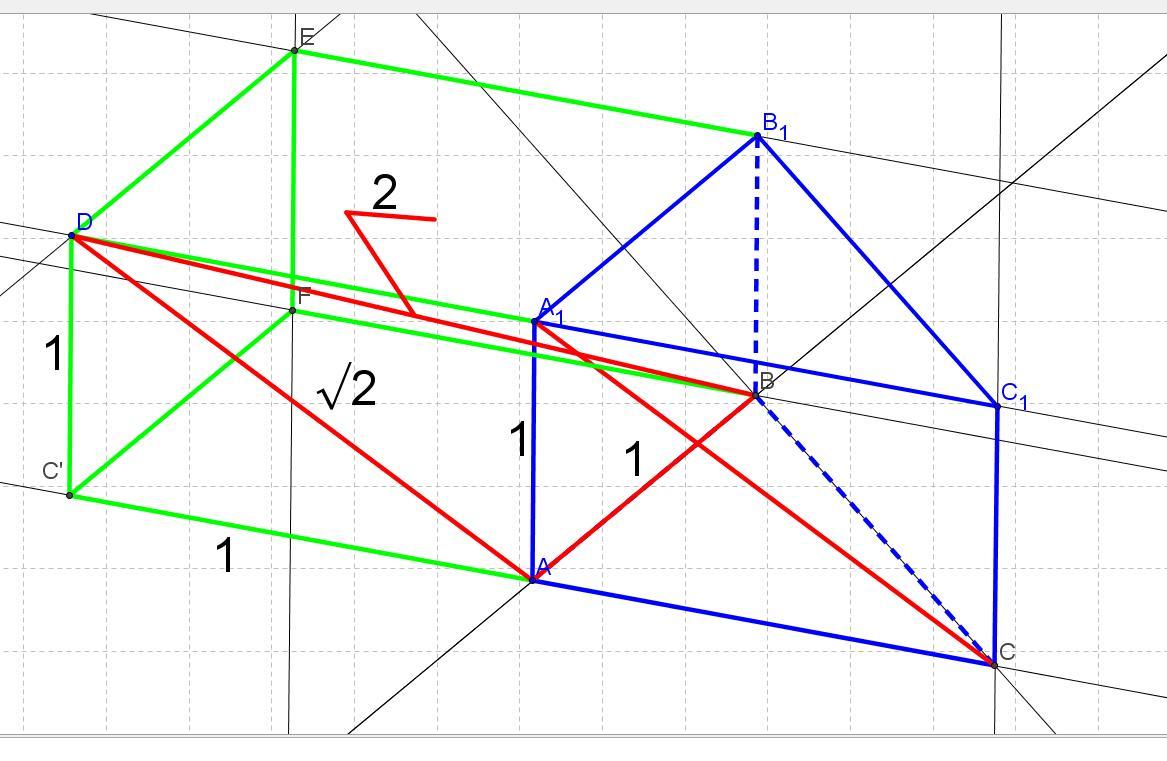
в правильной треугольной
призме АВСА1В1С1, все ребра
которой равны 1, найдите угол
между прямыми АВ и СA1.
Ответы
В правильной треугольной призме АВСА1В1С1, все ребра
которой равны 1, найдите угол между прямыми АВ и СA1.
В этой задаче есть 2 варианта решения:
1) геометрический,
2) аналитический.
1) Угол между заданными скрещивающимися прямыми можно определить, если отрезок СА1 переместить параллельно себе из точки С в точку А. Получим отрезок AD.
Соединив точки В и D, получаем треугольник AВD и в нём искомый угол ВАD.
Отрезок АD как диагональ квадрата равен √2.
Угол C'AD равен 180 – 60 = 120 градусов.
Диагональ С’B = √(1² + 1² - 2*1*1*(-1/2) = √3, а отрезок ВD по Пифагору равен:
ВD = √(1 + 3) = √4 = 2.
По теореме косинусов находим косинус угла ВАD.
cos BAD = √(1² + (√2)² - 2²)/(2*1*√2) = -1 / (2√2) = -√2 / 4 ≈ -0,35355.
Угол равен arccos(-√2 / 4) = 1,93216 радиан или 110,7048 градуса.
2) Определяем координаты точек.
А(0; 0; 0), В(0,5; √3/2; 0).
Вектор АВ = ((0,5; √3/2; 0), модуль равен 1.
C(1; 0; 0). A1(0; 0; 1).
Вектор СА1 = (-1; 0; 1), модуль равен √2.
cos BAD = (0,5*(-1)+(√3/2)*0+0*1)/(1*√2) = -1/(2*√2)= -√2 / 4 ≈ -0,35355.
Угол равен arccos(-√2 / 4) = 1,93216 радиан или 110,7048 градуса.