Предмет: Алгебра,
автор: warladno
Срочно зделаите задание 15!!!! Подробно расписать решение!(но не жирно)
Приложения:
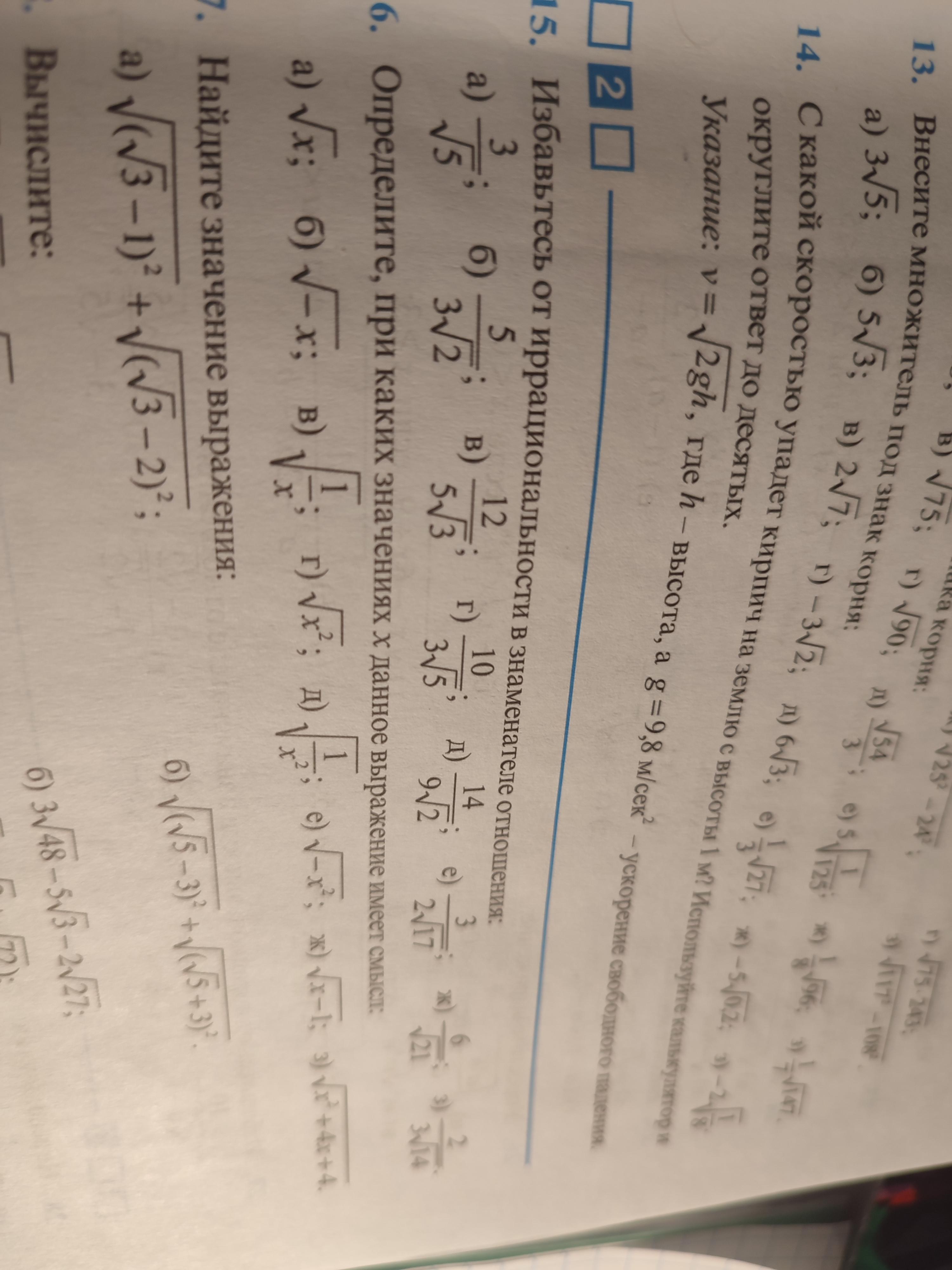
Ответы
Автор ответа:
1
Ответ:
Дробь не измениться, если числитель и знаменатель дроби умножить на одно и то же число . Будем умножать на соответствующий корень , так как .
warladno:
Спасибо большое.
Похожие вопросы
Предмет: История,
автор: svetlanaladugina22
Предмет: История,
автор: alinapilipiv11
Предмет: Физика,
автор: ivanna28062008
Предмет: Математика,
автор: FallendeLone
Предмет: Алгебра,
автор: ivanpelepenka