Предмет: Алгебра,
автор: kimkarina953
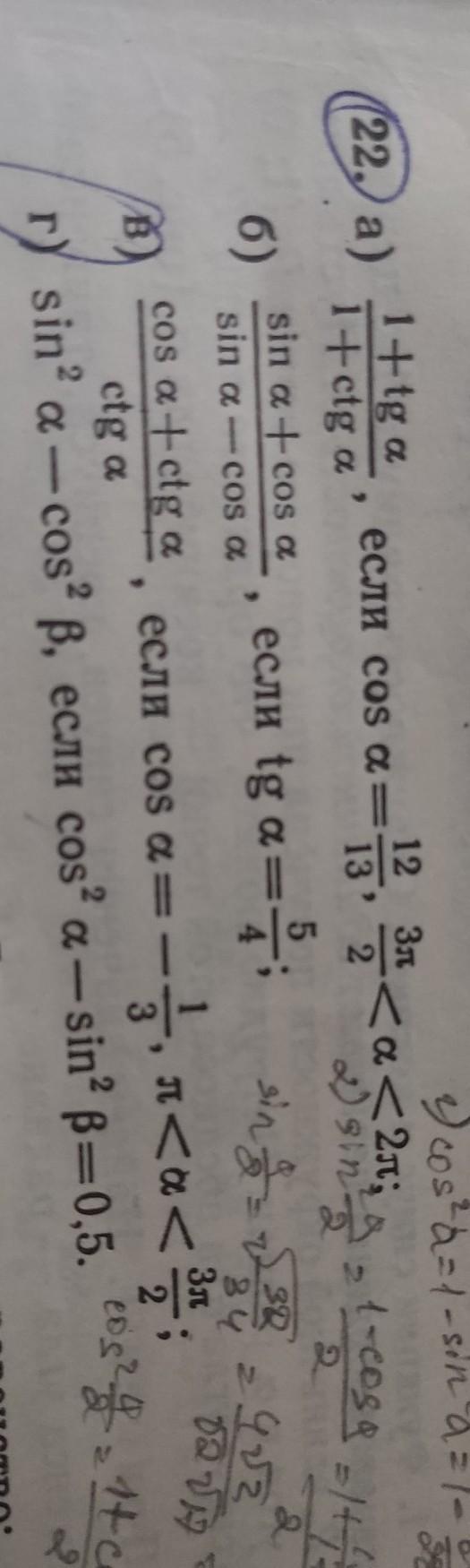
помогите пожалуйста с алгеброй пожалуйста
Приложения:
Ответы
Автор ответа:
1
Universalka:
Нет, в это время не смогу .
Похожие вопросы
Предмет: Математика,
автор: do78a868
Предмет: МХК,
автор: beregnouslava
Предмет: История,
автор: khryss
Предмет: Математика,
автор: kimnatlia0
Предмет: Право,
автор: vovabricz