Предмет: Математика,
автор: koshakautist
математика 10 класс 3 примера помогите пожалуйста, хотябы ответы без решения напишите
Приложения:
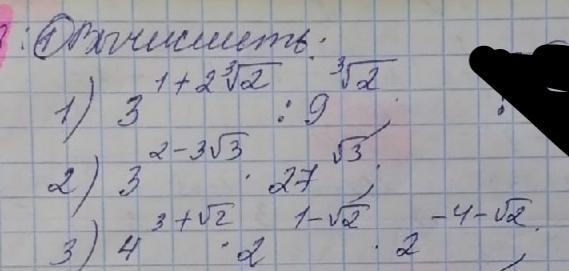
Ответы
Автор ответа:
1
Ответ:
1)
2)
3)
Пошаговое объяснение:
Вычислить:
1)
Воспользуемся правилом:
2)
Еще одно правило:
3)
Правила все написаны. Посчитаем.
Похожие вопросы
Предмет: Литература,
автор: anastasiyaBlack
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: marianamurnaeva2011
Предмет: Английский язык,
автор: kristinage22
Предмет: Русский язык,
автор: Daniiltih0