Предмет: Алгебра,
автор: Kirofeed
Помогите решить уравнение третьей степени лучшим способом
Приложения:
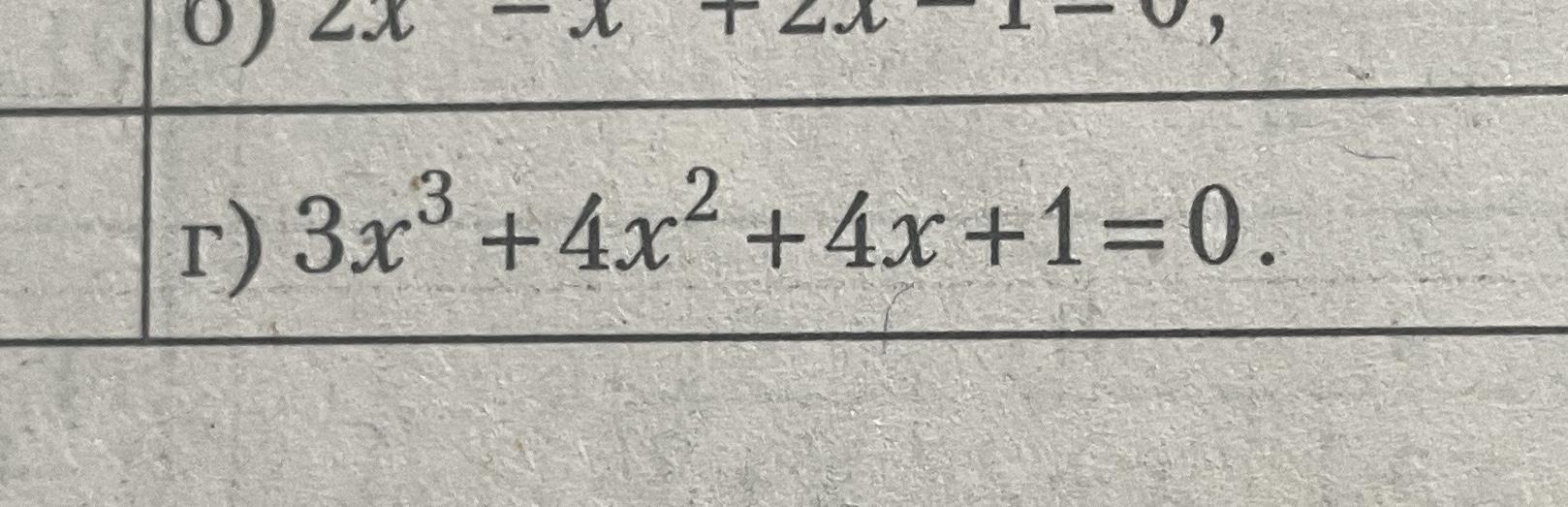
Ответы
Автор ответа:
1
Ответ:
Объяснение:
- квадратный трехчлен, который раскладывается на множители таким способом:
, где x1 и x2 - корни уравнения
В этом случае:
Как можно увидеть, не имеет корней, так как дискриминант отрицательный, значит в уравнении
3x+1 равно 0, значит
Автор ответа:
0
Ответ:
Объяснение:
Приравниваем каждую скобку к нулю
Выходит данное уравнение третьей степени имеет один действительный корень
Похожие вопросы
Предмет: Химия,
автор: andriyRT
Предмет: Другие предметы,
автор: masa42964
Предмет: Немецкий язык,
автор: nigggzhshdhd
Предмет: Химия,
автор: Moon777777
Предмет: Математика,
автор: vatyavatin93