Предмет: Геометрия,
автор: valenlina10
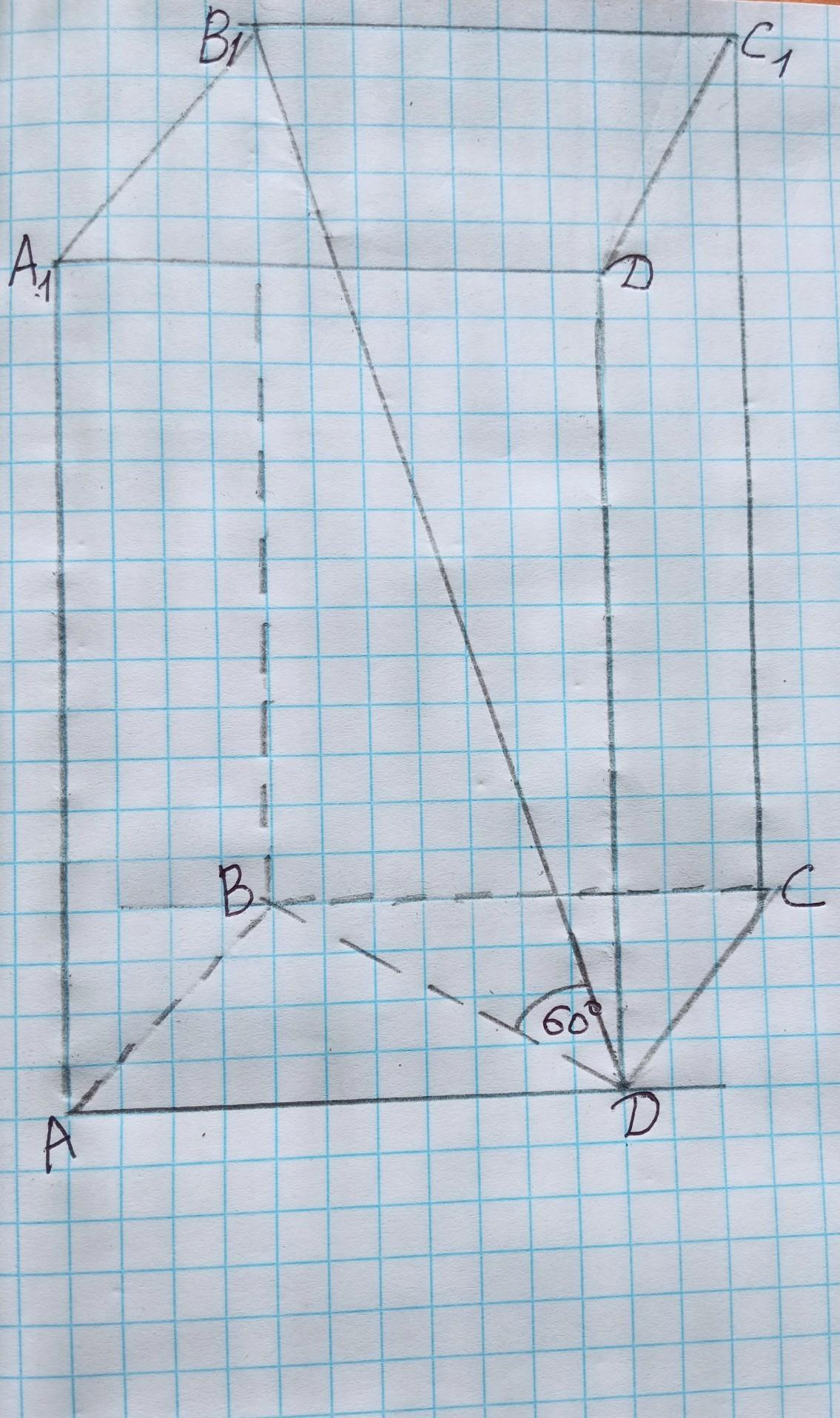
У правильній чотирикутній призмі сторона основи дорівнює 10 см, а діагональ утворює з площиною основи кут 60°. Установіть відповідність:
1. Діагональ основи А. 10√3 см
2. Діагональ призми Б. 10√6 см
3. Висота призми В. 20√2 см
4. Діагональ бічної грані Д. 10√7 см
Буду вдячний, якщо розпишите повністю кожне завдання, дякую!
Приложения:
BMW52:
4. Діагональ бічної грані Д. 10√7 см
Дякую
Если был бы чертёж, то было бы решение.
есть рисунок
Так прикрепите.
сделал
Привет. Ещё нужно?
Ответы
Автор ответа:
14
1. Найдем диагональ основания из прямоугольного △AВD по теореме Пифагора:
ВD= √(AB² + AD²) = √(10² + 10²) = =10√2(см).
2.Рассмотрим △В₁ВD- прямоугольный, тк призма правильная
∠ВВ₁D= 90 - 60°=30°(по тереме о сумме острых углов прямоугольного треугольника);
Тогда диагональ призмы
В₁D= 2*10√2=20√2( см).
3.△В₁ВD - прямоугольный, по теореме Пифагора найдём высоту призмы:
ВВ₁= √(В₁D² -ВD²) = √(400*2- 100*2) = =√600=10√6(см).
4. Всё боковые грани правильной призмы равные прямоугольники, диагонали которых равны. △АВВ₁-прямоугольный.По теореме Пифагора:
AВ₁ = √(AВ² + ВВ₁²) = √(100+ 100*6) = √700 =10 √7( см) .
Ответ.4. Діагональ бічної грані Д. 10√7 см.
Очень благодарен вам
Почему один балл?
извините, случайно нажал на 1 звёздочку
Похожие вопросы
Предмет: Психология,
автор: chortenya
Предмет: Математика,
автор: masha25152515
Предмет: Геометрия,
автор: nekrasovsergo451
Предмет: Обществознание,
автор: matveiizhokin
Предмет: Английский язык,
автор: art88170