Предмет: Геометрия,
автор: Аноним
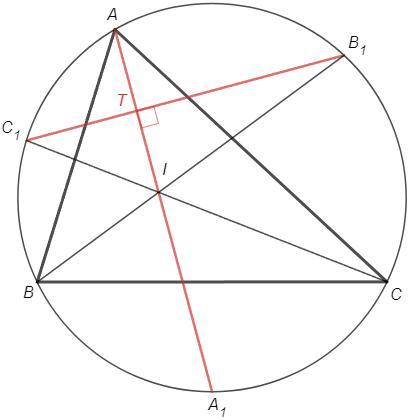
6.Прямі, які містять бісектриси трикутника ABC, перетинають його описане коло в точках А1, В1, С1. Доведіть, що центр вписаного кола трикутника АВС є ортоцентром трикутника А1 В1 С1.
Приложения:

Ответы
Автор ответа:
1
Вершины ABC разбивают окружность на три дуги.
◡AB+◡BC+◡AC=360°
Биссектрисы делят эти дуги пополам.
◡AC1 +◡A1C +◡CB1 =180°
Угол между хордами равен полусумме дуг.
∠T =(◡AC1 +◡A1B1)/2 =180°/2 =90°
Прямая AA1 содержит высоту к стороне B1C1 треугольника А1В1С1.
Аналогично BB1 и СС1.
Таким образом прямые, содержащие биссектрисы ABC, содержат высоты A1B1C1.
Тогда инцентр ABC является ортоцентром A1B1C1.
Приложения:
siestarjoki:
∠ATC1=∠A1TB1 =(◡AC1+◡A1B1)/2
∠ATB1=∠A1TC1 =(◡AB1+◡A1C1)/2
Похожие вопросы
Предмет: Английский язык,
автор: shu586437
Предмет: Математика,
автор: masakhomiak2010
Предмет: Українська мова,
автор: alexandrbukur
Предмет: Биология,
автор: dasha147ka
Предмет: География,
автор: arisakova2008