Предмет: Геометрия,
автор: marickaversler
знайдіть координати четвертої вершини паралелограма abcd якщо a(0;0) b(7;2) c(x;y) d(-2;-4) знайти суму цих координат
100б
Ответы
Автор ответа:
1
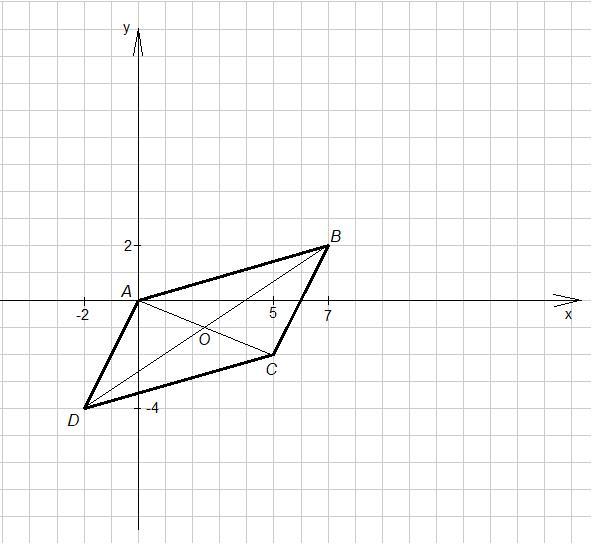
Ответ:
C(5; - 2)
Объяснение:
- Диагонали параллелограмма точкой пересечения делятся пополам.
Пусть О(x₀; y₀) - точка пересечения диагоналей параллелограмма ABCD.
Тогда О - середина BD.
- Координаты середины отрезка равны полусумме соответствующих координат его концов.
O(x₀; y₀)
B(7; 2), D(- 2; - 4)
O(2,5; - 1)
Но точка О также середина отрезка АС.
А(0; 0), С(х; у)
x = 5
y = - 2
C(5; - 2)
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: gomokievgenia
Предмет: Другие предметы,
автор: angely33615
Предмет: Английский язык,
автор: emaeept
Предмет: Математика,
автор: ktotoktonibud68
Предмет: Химия,
автор: hipphhhhjjjjjjjjj