Предмет: Математика,
автор: akkdeleteqpwmfj
Помогите
Обчислить интеграл
Приложения:
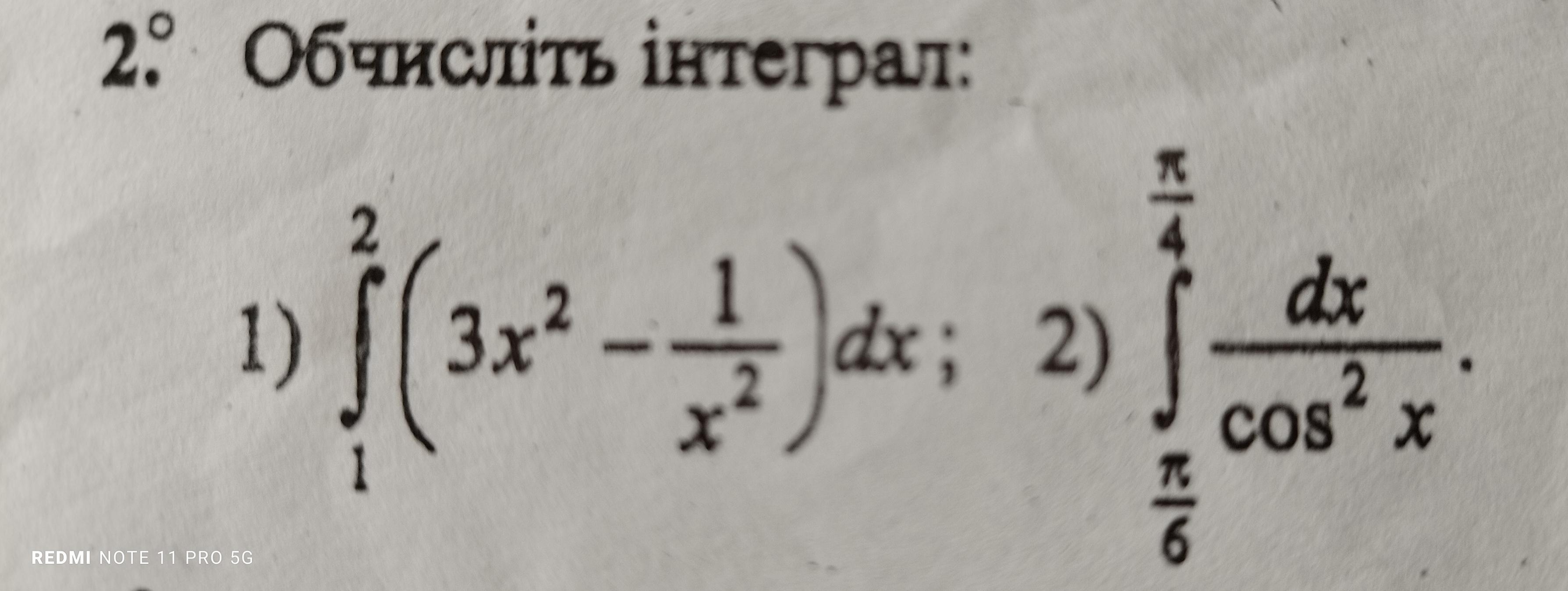
Ответы
Автор ответа:
0
Решение и ответ:
Похожие вопросы
Предмет: Алгебра,
автор: sasenkauwu
Предмет: Физика,
автор: Yuna2811
Предмет: Математика,
автор: milkytal
Предмет: Химия,
автор: gorivady26
Предмет: Биология,
автор: anastasiam026