График квадратичной функции, даю 100 баллов
Ответы
Ответ:
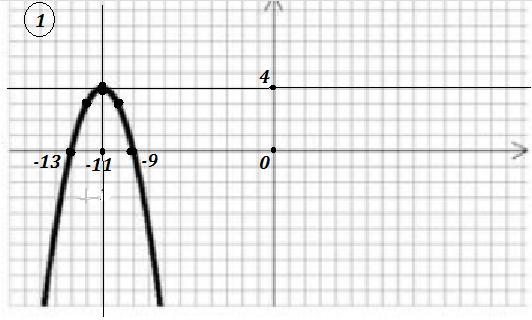
Парабола имеет коэффициент a= -1 , проходит через точки (-10;3) и (-12;3) .
Вершина параболы находится в точке с координатами ( -11 ; 4 ) . Поэтому заданная парабола - это парабола , сдвинутая по оси ОХ влево на 11 единиц и по оси ОУ вверх на 4 единицы .
Её уравнение имеет вид . Раскроем скобки.
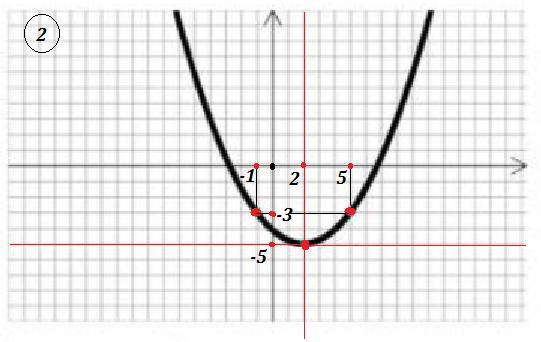
Парабола проходит через точки (-1;-3) и (5;-3) . Поэтому коэффициент а не будет равен 1 > 0 (ветви вверх) . ( Если бы было а=1 , то парабола проходила бы через точки (1;-4) и (3;-4) ) .
Вершина параболы находится в точке с координатами ( 2 ; -5 ) . Поэтому заданная парабола - это парабола , сдвинутая по оси ОХ вправо на 2 единицы и по оси ОУ вниз на 5 единиц .
Её уравнение имеет вид .
Чтобы найти коэффициент а , подставим координаты какой либо из точек (-1;-3) или (5;-3) в это уравнение.
Уравнение параболы имеет вид: . Или, если раскрыть скобки, то
.
Замечание. Можно было сразу координаты трёх точек , перечисленных выше, принадлежащих параболе, подставить в исходное уравнение . Тогда бы пришлось решать систему трёх линейных уравнений .