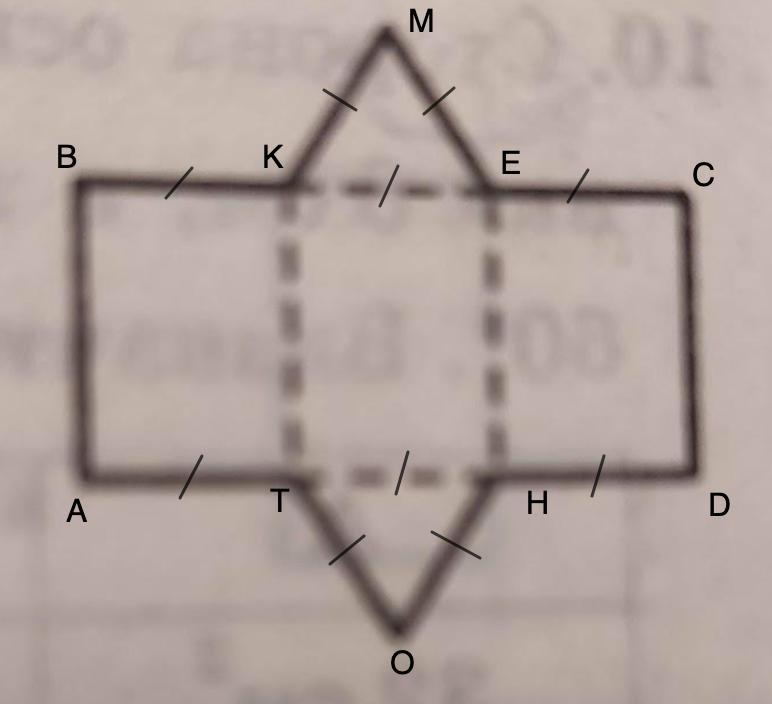
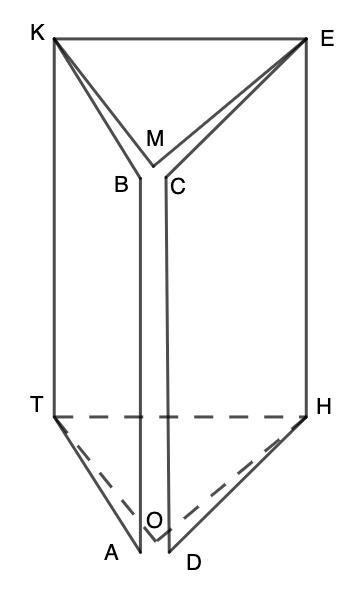
На рисунку зображено розгортку правильної трикутної призми. Визначте площу бічної поверхні цієї призми, якщо периметр розгортки дорівнює 68 см, а периметр основи - 18 см.
Ответы
Ответ:
Площадь боковой поверхности этой призмы равна 180 см².
Объяснение:
На рисунке изображена развертка правильной треугольной призмы. Определите площадь боковой поверхности этой призмы, если периметр развертки равен 68 см, а периметр основания - 18 см.
Дано: развертка правильной треугольной призмы.
Росн.= 18 см; Рразв. = 68 см.
Найти: Sбок.
Решение:
- Периметр - сумма длин всех сторон.
- Основания правильной треугольной призмы - равносторонние треугольники.
⇒ Р(КМЕ) = Р(ТНО) = 18 см
Тогда сторона основания равна:
КМ = МЕ = КЕ = ТН = ТО = ОН = 18 : 3 = 6 (см)
Так как нам дана развертка правильной призмы, то
ВК = КМ = 6см; ЕС = МЕ = 6 см; АТ = ТО = 6 см; HD = HO = 6 см.
Пусть АВ = CD = h.
Pразв. = АВ + ВК + КМ + МЕ + ЕС + CD + DH + HO + OT + AT = 68 (см)
2h + 48 = 68
2h = 20
h = 10
⇒ АВ = CD = h = 10 см.
- Площадь прямоугольника равна произведению смежных сторон.
Sбок. = S(ABCD) = AB · CD = 10 · (6 + 6 +6) = 180 (см²)
Площадь боковой поверхности этой призмы равна 180 см².
#SPJ1