Предмет: Геометрия,
автор: prin4ik
Розв'язати задачу. Проекції катетів прямокутного трикутника на гіпотенузу дорівнюють 12 см і 27 см. Знайти катети
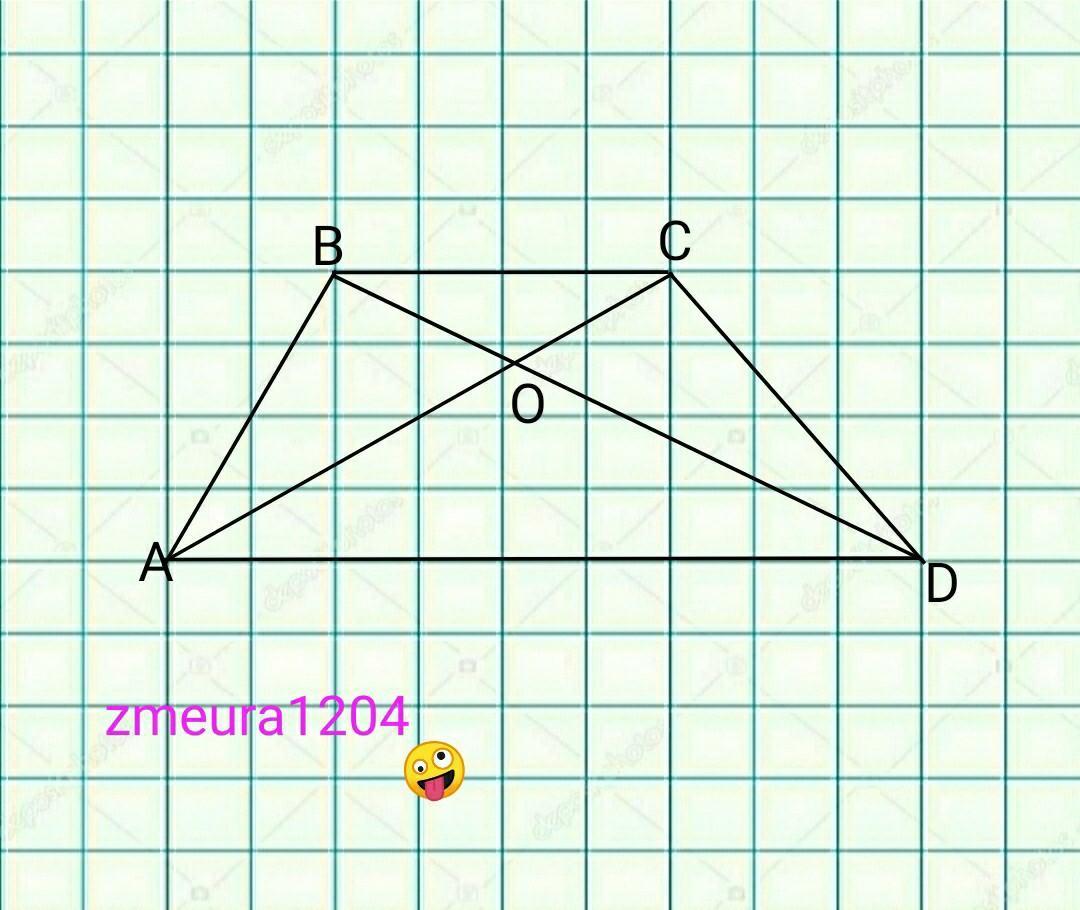
Розв'язати задачу. Дано : АВСD - трапеція, О - точка перетину діагоналей АС і ВD. Довести, що трикутник ВОС подібний до трикутника DOA.
Ответы
Автор ответа:
1
Объяснение:
1)
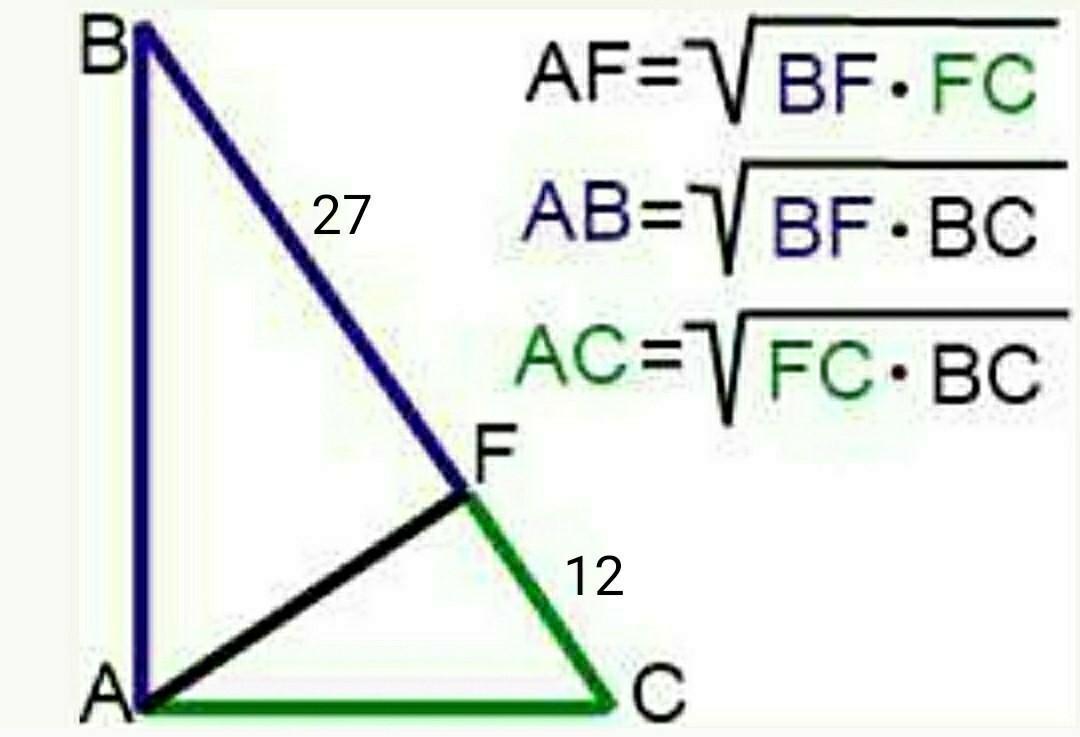
∆АВС- прямокутний трикутник;
∠ВАС=90°
FC=12см проекція катета АС на гіпотенузу ВС
FB=27см проекція катета АВ на гіпотенузу ВС
ВС=FC+FB=12+27=39см
Пропорційні відрізки прямокутного трикутника:
АС=√(FC*BC)=√(12*39)=√(3*4*3*13)=3*2√13=6√13 см
АВ=√(FB*BC)=√(27*39)=√(3*9*3*13)=3*3√13=9√13см
Відповідь: AC=6√13см; АВ=9√13см
_____
2)
∠ВОС=∠АОD, вертикальні кути.
∠АСВ=∠САD, внутрішні навхрест лежать при паралельних прямих ВС||AD, січною АС.
Тож двох рівних кутів достатньо.
∆ВОС~∆DOA, за двома кутами.
_________
P.s.
(∠DBC=∠BDA, так само внутрішні навхрест лежать при паралельних прямих ВС||AD, січною BD)
Приложения:
Похожие вопросы
Предмет: Химия,
автор: anitafomenko0906
Предмет: Русский язык,
автор: mmehin32
Предмет: Қазақ тiлi,
автор: nikoletta87
Предмет: Українська література,
автор: anonimckputuu