Question

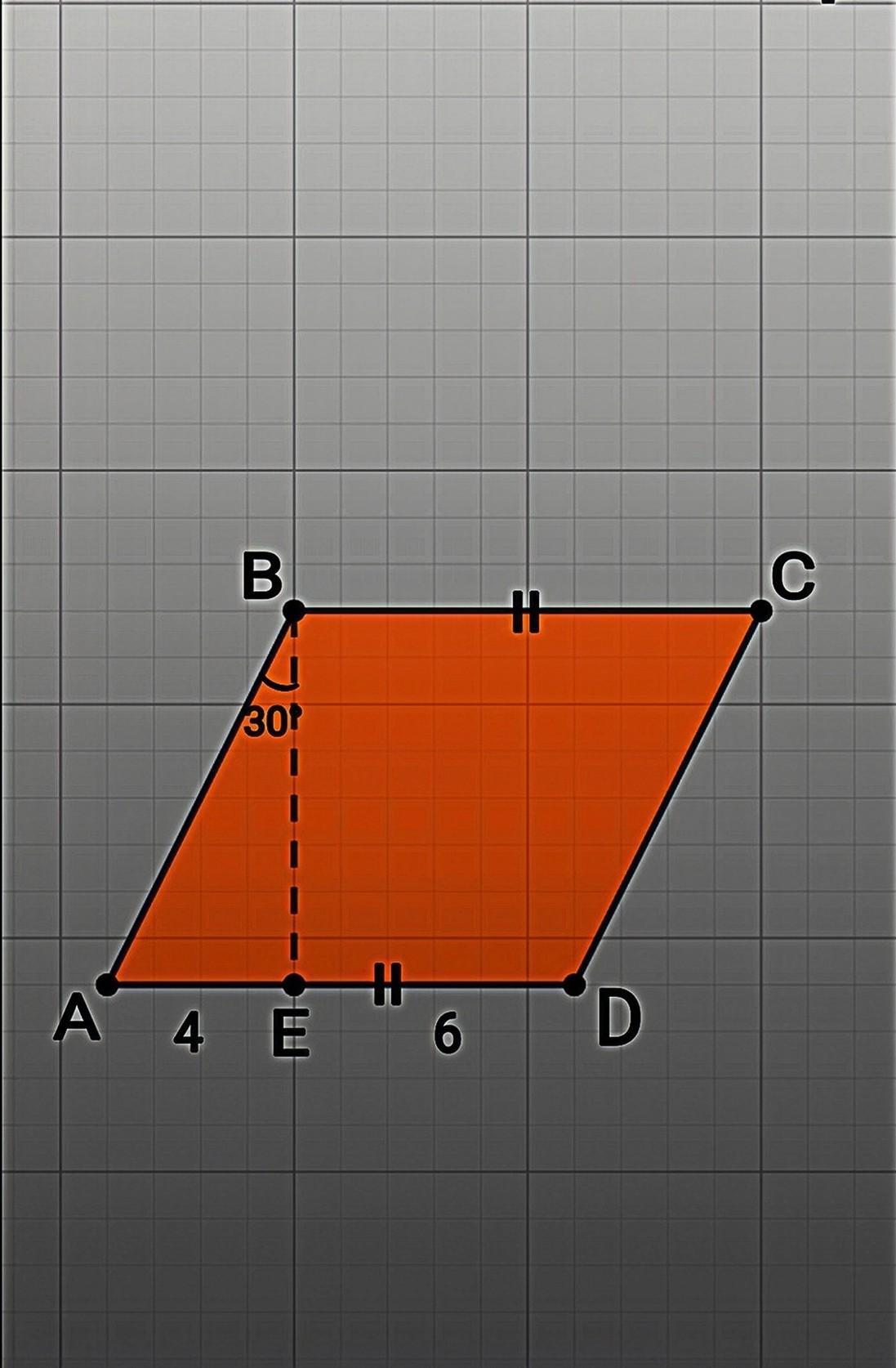
Высота ВЕ параллелограмма ABCD образует со стороной АВ угол 30 градусов и делит сторону AD на отрезки АЕ = 4см и DE = 6cм. Найти площадь параллелограмма.

Answer 1

Ответ:

40√3см²

Объяснение:

Дано: ABCD – параллелограмм, ВЕ – высота, ∠АВЕ = 30°, АЕ = 4см, DE = 6см

Найти: $\displaystyle S_{ABCD} -?$

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

• Рассмотрим ∆АВЕ – прямоугольный. Катет АЕ лежит против угла в 30°. Значит равен половине гипотенузы. АВ = 2АЕ ⇒2 * 4 = 8см.
• Высота ВЕ также является катетом ∆АВЕ. Согласно теореме Пифагора:

⠀⠀⠀АЕ² + ВЕ² = АВ²

⠀⠀⠀16 + ВЕ² = 64

• Отсюда катет(ВЕ) равен:

⠀⠀⠀ВЕ = √(64-16)

⠀⠀⠀ВЕ = √48

⠀⠀⠀ВЕ = √(12 * 3)

⠀⠀⠀ВЕ = 4√3см.

• Площадь параллелограмма равен произведению высоты на ту сторону, к которой он проведён. AD = AE + ED ⇒4 + 6 = 10см

⠀⠀⠀$\displaystyle S_{ABCD}=10 \:*\:4\sqrt{3}=\bf40$см²

Ответ: площадь параллелограмма АВСD равен 40√3см²