Предмет: Алгебра,
автор: nastamyravska
область визначення СРОЧНООООО
(кожне окремо , з поясненням)
Приложения:
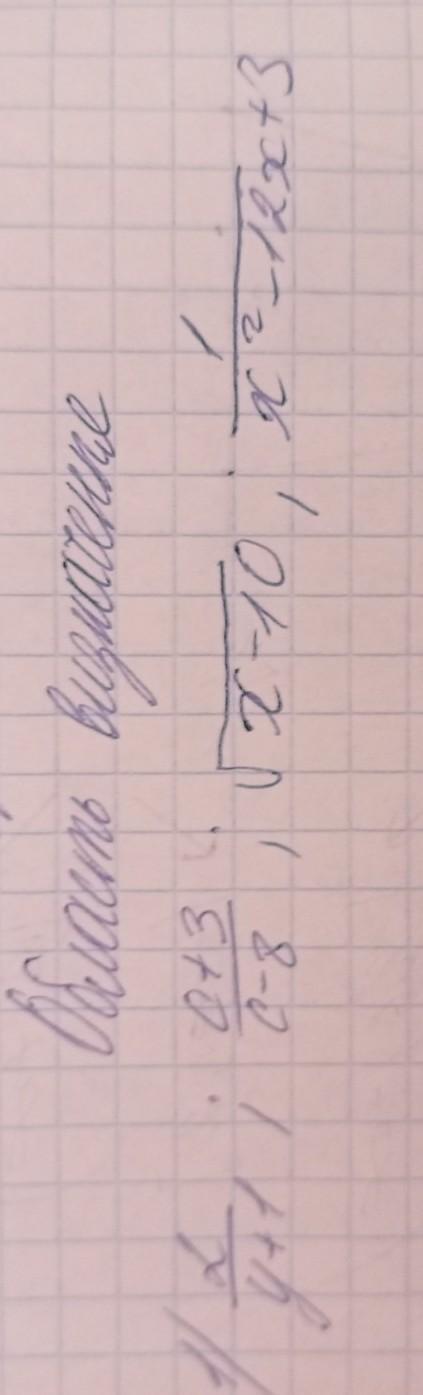
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Это пример тогда, когда есть дробь. Когда есть дробь, надо требовать чтобы знаменатель (то, что под дробью) не был равен нулю, так как на ноль делить нельзя!
Пример, аналог. примеру 1.
Это пример с корнем. Нужно требовать, чтобы подкоренное выражение не было отрицательным (т.е. ).
Дальше, по формуле корней находим корни
Эти корни не принадлежат ОДЗ, т.е
Похожие вопросы
Предмет: Химия,
автор: dr027851
Предмет: Информатика,
автор: demidkoningen
Предмет: Українська література,
автор: elenanerushenko1977
Предмет: Математика,
автор: levmt022
Предмет: География,
автор: lipka8