Предмет: Алгебра,
автор: anelmukasheva95
решите графическим способом систему уравнений. очень срочно!!
Приложения:
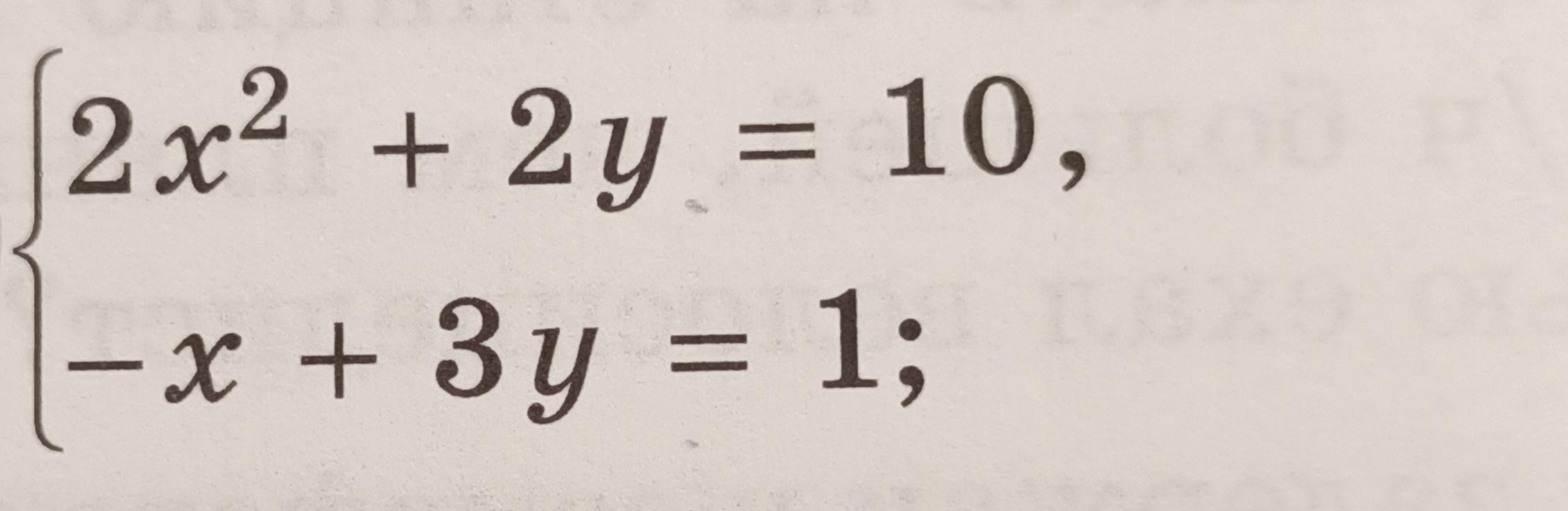
Ответы
Автор ответа:
1
Ответ:
Ответ: (-2,3; -0,4), (2; 1)
Объяснение:
Решить систему графическим способом:
Для того, чтобы решить систему графическим способом, надо построить графики. Координаты точек пересечения этих графиков и будут решениями данной системы.
В обоих уравнениях выразим у:
1.
- квадратичная функция, график - парабола, ветви вниз.
Координаты вершины (0; 5)
Возьмем несколько точек:
Строим график.
2.
- линейная функция, график - прямая.
Для построения достаточно 2-х точек:
Строим график.
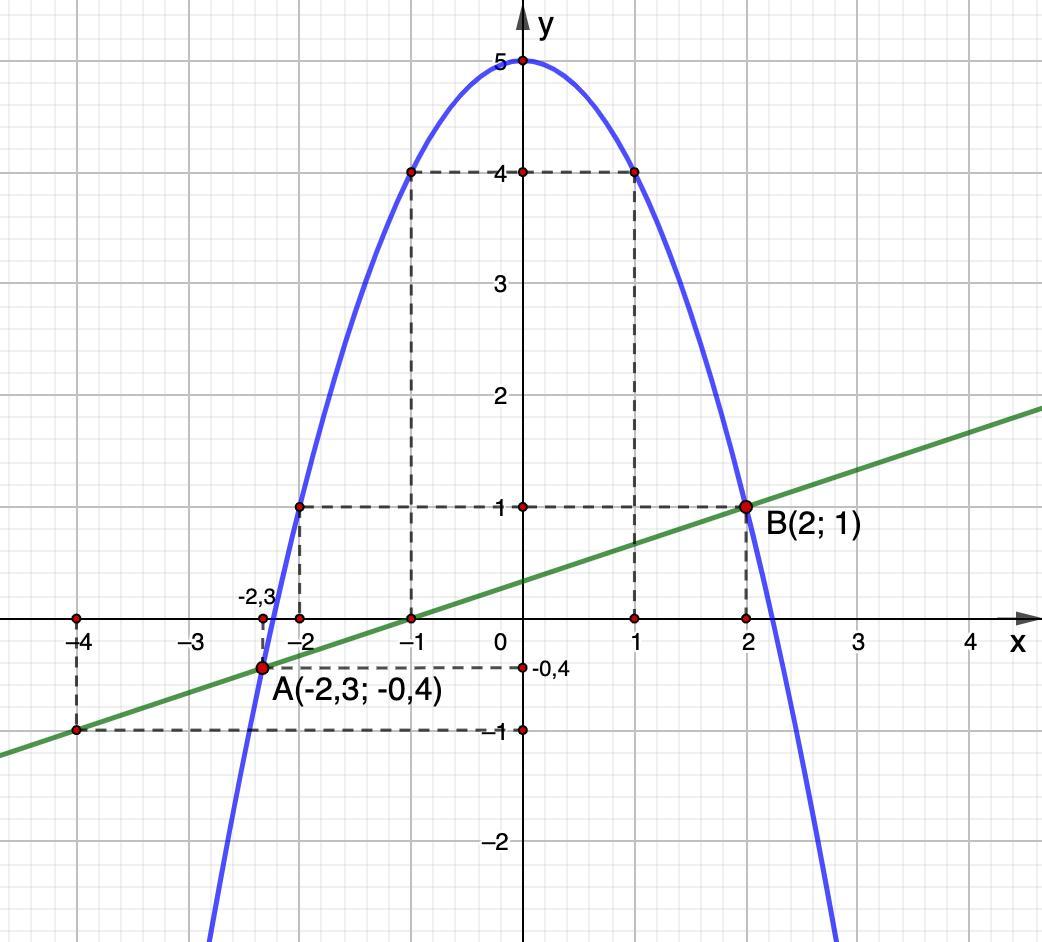
Получили две точки пересечения:
А(-2,3; -0,4), В(2; 1).
Ответ: (-2,3; -0,4), (2; 1)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kamillabukanova437
Предмет: Қазақ тiлi,
автор: boranbaevaerkenaz056
Предмет: Английский язык,
автор: holoden935
Предмет: Русский язык,
автор: theprincess492
Предмет: Английский язык,
автор: savinyhp6