Предмет: Алгебра,
автор: ijs251207
срочно помогите срочно помогите срочно помогите
Приложения:
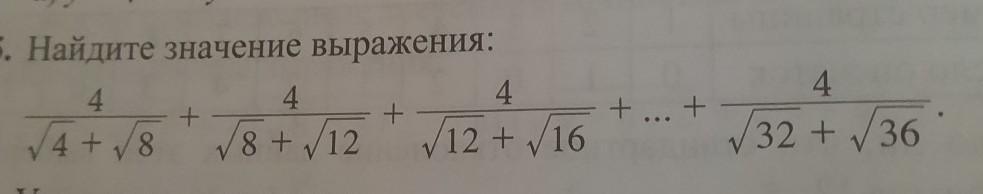
Ответы
Автор ответа:
2
Ответ: 4 .
Домножим дроби на выражения, сопряжённые знаменателям, и вынесем 4 за скобку . Потом воспользуемся формулой разности квадратов: .
makmutaziza:
здравствуйте, можете помочь мне с алгеброй 10 класс, вопрос у меня в профиле в разделе вопросы.
пожалуйста прошу
помогите
дам хороший бонус
помогите с алгеброй,прошу!!!
Помогите с алгеброй, очень нужно,буду очень благодарна!!!!
Похожие вопросы
Предмет: Русский язык,
автор: kica58
Предмет: Русский язык,
автор: 982alex
Предмет: Английский язык,
автор: wikt18
Предмет: География,
автор: anyasozykina04
Предмет: Математика,
автор: alena361832