Предмет: Геометрия, автор: grinshyk

Ещё немного помощи нужно ♥️ , спасибо.

Приложения:

zmeura1204: :)

zmeura1204: 16-8=8 проекція бокової сторони на нижню основу. Теорема Піфагора h=√(17²-8²)=15; S=h(a+b)/2=15(8+16)/2=15*24/2=180

zmeura1204: 8) 24:2=12 половина основи; теорема Піфагора: h=√(13²-12²)=5; S=5*24/2=60

zmeura1204: 9) S=d1*d2/2=12*16/2=96; теорема Піфагора: а=√((d1/2)²+(d2/2)²)=√(12²/4+16²/4)=√(36+64)=√100=10; P=4a=4*10=40

Ответы

Автор ответа: TanomiU

Ответ:

Объяснение:

Дано:

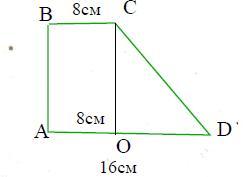
ABCD - прямоуг. трапеция

ВС = 8см
AD = 16см

CD = 17см

---------------

Sтр. - ? см²

1) Опустим из вершины трапеции С высоту CO на основание AD.

Получили прямоугольник АВСO, в котором ВС = АО = 8см

Тогда OD = 16 - 8 = 8(см)

2)Рассмотрим прямоугольный ΔСOD ( т.к. СО -высота)

CD = 17(см) по условию, OD = 8см ( по решению)

По т.Пифагора, квадрат гипотенузы равен сумме квадратов катетов, поэтому

CD² = CО² + OD², откуда

СО² = CD² - OD² = 17² - 8² = 289 - 64 =225 (см²)

СО = √225 = 15 (см) = dscjnf nhfgtwbb

3) Найдем площадь трапеции:

Sтр. = ¹/₂h(BC + AD) = ¹/₂*15*(8+16) = 15*12 = 180см²

____________________________

Дано:

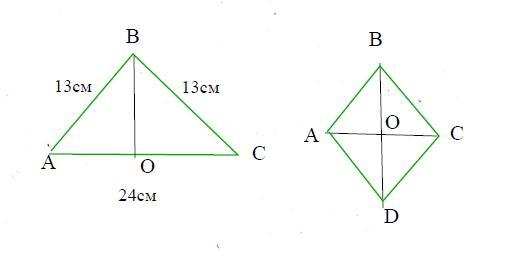
АВС - равнобедренный треугольник

АВ =ВС = 13см

АС = 24см

S = ?см²

-------

1) Из вершины В ΔАВС опустим высоту ВО на основание АС.

Высота в равнобедренном Δ-ке является одновременно медианой и биссектрисой этого Δ-ка. Поэтому

АО=ОС = 24/2 = 12см

2) из прямоугольного ΔАВО найдем по т.Пифагора высоту ВО:

ВО² = АВ² - АО² = 13² - 12² = 169 - 144 =25(см²)

ВО = √25 = 5 (см)

3) Найдем площадь Δ-ка АВС:

S = ¹/₂ ВО*АС = 5*24/2 = 60(см²)

----------------------------------

Дано:

ABCD - ромб
АС = 12см

BD = 16см

Р - ?см

S -? см²

-------

Свойство ромба:

Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.

Пусть диагонали ромба ABCD пересекаются в т.О

1) Рассмотрим один из 4-х полученных треугольников, например, ΔАОВ:

По свойству ромба:

ВО = BD/2 =16/2 = 8(см)

АО = АС/2 = 12/2 = 6(см)

Найдем площадь этого Δ-ка:

S₁ = АО*ВО/2 = 6*8/2 = 24(см²) - площадь одного треугольника.

Ромб состоит из 4-х таких Δ-ков, поэтому

Sромба = 24 *4 = 96(см²)

2) Из Δ-ка АОВ по т.Пифагора найдем гипотенузу или сторону ромба АВ:

АВ² = АО² + ВО² = 6² + 8² = 36 + 64 = 100(см²)

АВ = √100 = 10(см) - одна сторона ромба.