Question

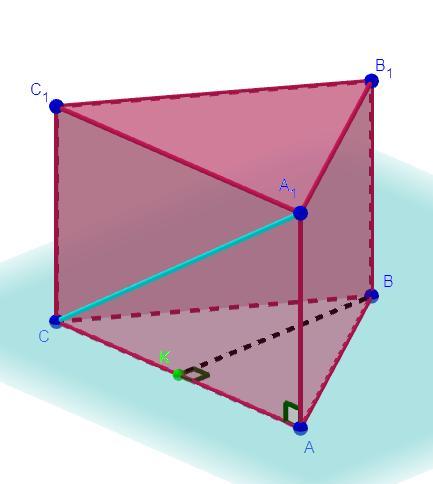
Основою прямої призми є рівнобедрений трикутник ABC, AB = BC = 5 см. Висота трикутника АВС дорівнює 4 см. Знайти діагональ бічної грані призми, яка містить основу трикутника, якщо висота призми дорівнює 8 см.​

Answer 1

Відповідь:

Діагональ бічної грані призми, яка містить основу трикутника дорівнює 10 см

Пояснення:

Дано: ABCA₁B₁C₁ - пряма призма, AB = BC = 5 см, BK ⊥ AC,

BK = 4 см, AA₁ = 8 см

Знайти: A₁C - ?

Розв'язання:

За властивістю прямої призми її бічні ребра є перпендикулярними до основи призми, отже AA₁ ⊥ BAC.

За означенням пряма перпендикулярна до площини перпендикулярна до будь-якої прямої, що лежить у цій площині, тоді

так як AA₁ ⊥ BAC і AC ⊂ ABC, то AA₁ ⊥ AC, отже трикутник ΔAA₁C - прямокутний.

Розглянемо прямокутний трикутник ΔBAK (BK ⊥ AC за умовою).

За наслідком з теореми Піфагора:

$AK = \sqrt{AB^{2} - BK^{2}} = \sqrt{5^{2} - 4^{2}} = \sqrt{25 - 16} = \sqrt{9} = 3$ см.

Розглянемо рівнобедрений трикутник ΔABC (AB = BC за умовою).

За теоремою висота рівнобедреного трикутника проведена до основи є медіаною і бісектрисою, тоді так як за умовою BK ⊥ AC

(BK - висота), то BK є медіаною і бісектрисою, як наслідок за означенням медіани AK = KC.

За основною властивістю відрізка:

AC = AK + KC і так як AK = KC, то AC = 2AK = 2 · 3 = 6 см.

Розглянемо прямокутний трикутник ΔAA₁C:

За наслідком з теореми Піфагора:

$A_{1}C = \sqrt{AC^{2} + AA_{1}^{2}} = \sqrt{6^{2} + 8^{2}} = \sqrt{36 + 64} = \sqrt{100} = 10$ см.