ДОПОМОЖІТЬ БУДЬ ЛАСКА!!!
Ответы
Ответ:
1. Смотрите доказательство в пункте "Объяснение"
2. Гипотенуза треугольника равна 28 см
Объяснение:
1.
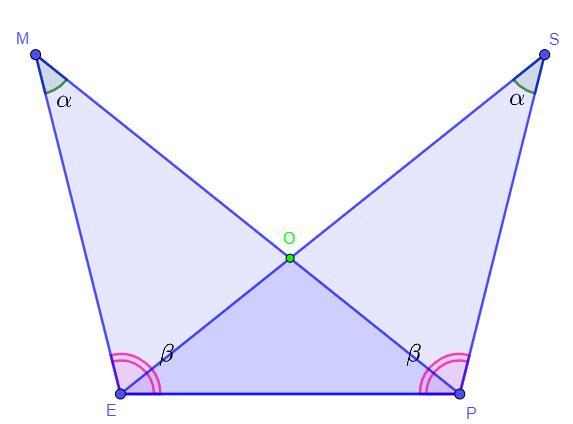
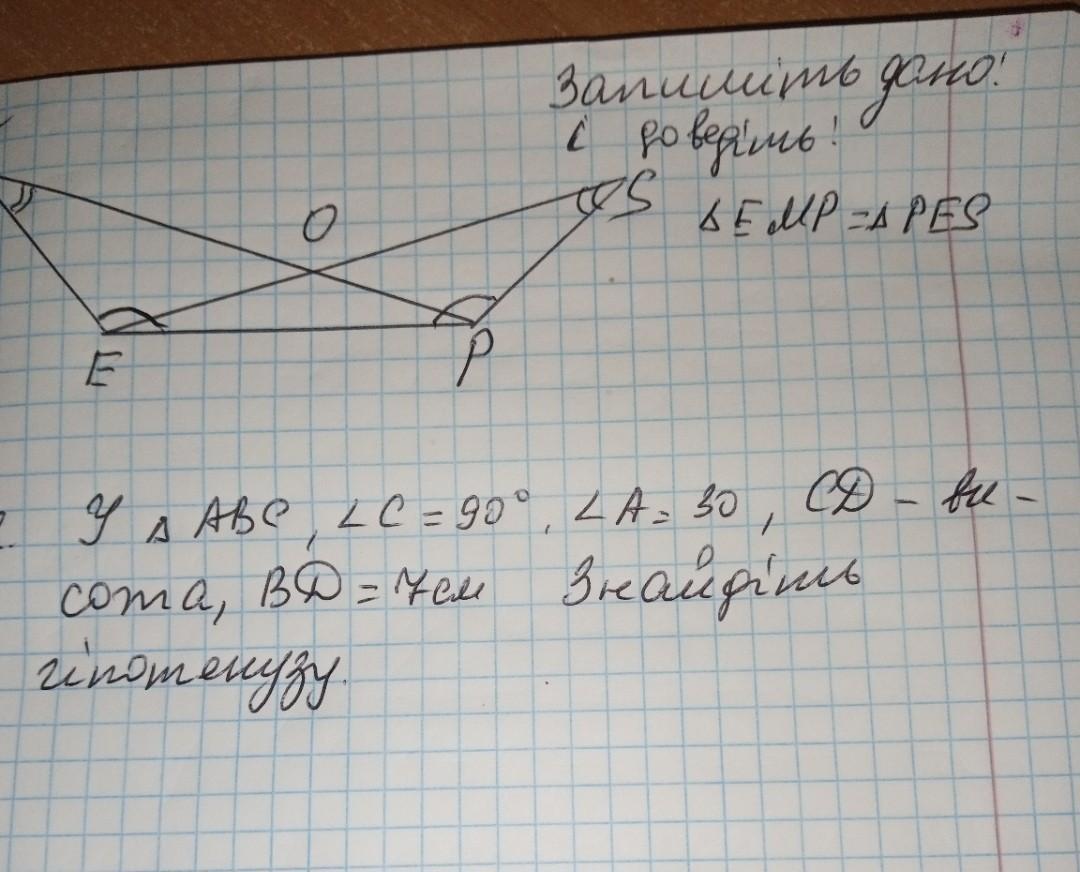
Дано: ∠PME = ∠PSE, ∠PEM = ∠EPS
Доказать: ΔEMP = ΔPES
Доказательство:
Пусть угол ∠PME = α, тогда ∠PSE = α, так как по условию
∠PME = ∠PSE и аналогично ∠PEM = β, тогда ∠EPS = β, так как по условию ∠PEM = ∠EPS.
По теореме про сумму углов треугольника (треугольник ΔPME):
∠PME + ∠PEM + ∠MPE = 180° ⇒ ∠MPE = 180° - ∠PME - ∠PEM =
= 180° - α - β.
По теореме про сумму углов треугольника (треугольник ΔPES):
∠PSE + ∠EPS + ∠PES = 180° ⇒ ∠PES = 180° - ∠PSE - ∠EPS =
= 180° - α - β.
Так как угол ∠PES = 180° - α - β и угол ∠MPE = 180° - α - β, то
угол ∠PES = ∠MPE.
Треугольник ΔEMP = ΔPES по второму признаку равенства треугольников, так как угол ∠PME = ∠PSE - по условию, угол
∠PES = ∠MPE и сторона PE - общая.
2.
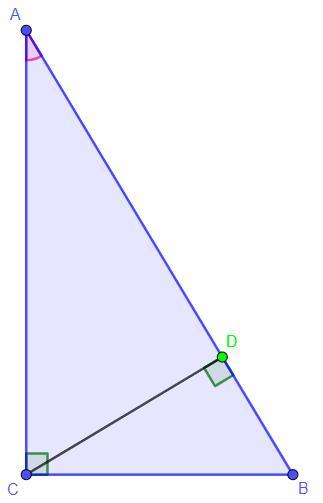
Дано: ∠BCA = 90°, ∠CAB = 30°, CD - высота, BD = 7 см
Найти: AB - ?
Решение:
По теореме про сумму углов треугольника (треугольник ΔABC):
∠BCA + ∠CAB + ∠CBA = 180° ⇒ ∠CBA = 180° - ∠BCA - ∠CAB =
= 180° - 90° - 30° = 60°.
Так как по условию CD - высота, то по определению CD ⊥ AB, следовательно треугольник ΔBDC - прямоугольный с прямым углом ∠CDB.
Рассмотрим треугольник ΔBDC.
По определению косинуса:
см.
Рассмотрим треугольник ΔABC.
По определению косинуса:
см.