Предмет: Математика,
автор: leonidbelokon57
Сторони паралелограма дорівнюють 5 і 4 см відповідно, а кут між ними складає 120°. Чому дорівнюють діагоналі паралелограма?
Ответы
Автор ответа:
1
Ответ:
Диагонали параллелограмма равны см и
см
Пошаговое объяснение:
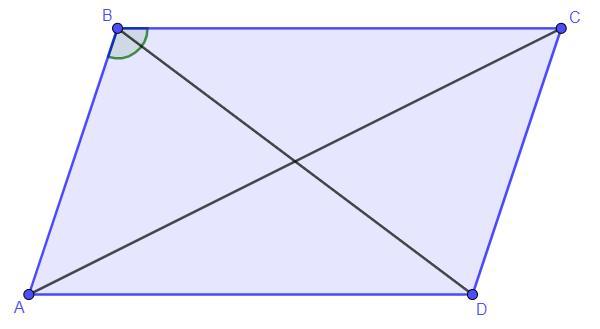
Дано: ABCD - параллелограмм, BC = 5 см, AB = 4 см
Найти: AC,BD - ?
Решение:
По следствию из теоремы косинусов для треугольника ΔABC:
см.
По тождеству параллелограмма (по условию ABCD - параллелограмм):
см.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: KirillBrian
Предмет: Русский язык,
автор: golyboglazya
Предмет: Русский язык,
автор: louiza1
Предмет: Алгебра,
автор: jebicox
Предмет: Математика,
автор: Ибрагим211