Высоты параллелограмма равны 3 и 4 см. Угол между ними равен 60°. Найдите большую сторону параллелограмма.
Ответы
Ответ:
Наибольшая сторона параллелограмма равна см
Объяснение:
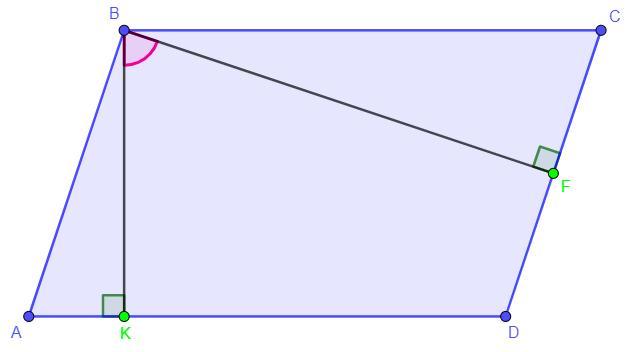
Дано: ABCD - параллелограмм, BK ⊥ AD, BF ⊥ CD, BK = 3 см,
BF = 4 см, ∠KBF = 60°
Найти: AB,BC - ?
Решение:
Так как по условию BK ⊥ AD и BF ⊥ CD, то угол ∠BKA = ∠BKD = 90° и угол ∠BFD = ∠BFC = 90°.
Четырехугольник BKDF - выпуклый, тогда по теореме сумма углов выпуклого четырех угольника равна 360°, следовательно
∠BKD + ∠BFD + ∠KBF + ∠ADC = 360° ⇒ ∠ADC =
= 360° - ∠BKD - ∠BFD - ∠KBF = 360° - 90° - 90° - 60° = 120°.
По определению параллелограмма (ABCD) его противоположные стороны параллельны, тогда AD║BC, угол ∠ADC и ∠BCD являются односторонними при параллельных прямых и секущей (AD║BC;ВС - секущая), следовательно по теореме угол ∠ADC + ∠BCD = 180° ⇒
⇒ ∠BCD = 180° - ∠ADC = 180° - 120° = 60°.
По свойствам параллелограмма (ABCD) его противоположные углы равны, тогда ∠BCD = ∠BAD = 60°.
Рассмотрим прямоугольный треугольник ΔBAK (по условию BK ⊥ AD):
По определению синуса в прямоугольном треугольнике:
см.
Рассмотрим прямоугольный треугольник ΔBCF (по условию BF ⊥ CD):
По определению синуса в прямоугольном треугольнике:
см.
Так как BC > AB , то наибольшая сторона параллелограмма это BC.